1. Алгебра
  2. Надо sin(arc tg2+arc tg3) ответ:

Надо sin(arc tg2+arc tg3) ответ: корень из 2/2 нужно само решение p.s. кто решит сделаю лучшим решением

эмилисенок2 эмилисенок2    3   18.03.2019 19:00    1

Ответы
Аркадий111111122222 Аркадий111111122222  26.05.2020 00:39

sin(arctg2+arctg3)=sin(arctg2)+sin(arctg3)

 

tga=sina/cosa,    следовательно

 

sina=tga*cosa,  поэтому

 

sin(arctga)=tg(arctga)*cos(arctga)=a*cos(arctga)

 

Найдём значение выражения cos(arctga):

 

Известна формула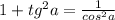   1+tg^{2}a=\frac{1}{cos^{2}a}

 

следовательно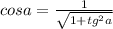        cosa=\frac{1}{\sqrt{1+tg^{2}a}}

 

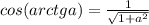
Значит:  cos(arctga)=\frac{1}{\sqrt{1+a^{2}}}

 

Итак,

 

sin(arctg2+arctg3)=sin(arctg2)+sin(arctg3)=

 

=2*\frac{1}{\sqrt{1+2^{2}}}+3*\frac{1}{\sqrt{1+3^{2}}}=\frac{2}{\sqrt{5}}+\frac{3}{\sqrt{10}}=\frac{2}{\sqrt{5}}+\frac{3}{\sqrt{5}*\sqrt{2}}=\frac{2\sqrt{2}+3}{\sqrt{10}}

 

 

 

 

 

 

 

 

 

 

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Kulkovadarya97 Kulkovadarya97  16.05.2021 21:12
За олфвець і три зошити заплатити 2,20 грн , а за 3 олівці і один зошит 1,8 грн, скільки коштує олівець і скільки коштує зошит ​...
ivanivankuznets ivanivankuznets  16.05.2021 21:12
Доведіть тотожність (a²+b²)×(a⁴‐a²b²+b⁴)‐(a³‐b³)×(a³+b³)=2b⁶​...
VERLIA VERLIA  16.05.2021 21:13
, sin x + 2 cos y = 2 3sin x – 4cos y=1....
volk910 volk910  16.05.2021 21:13
Знайдіть перший член та різницю арифметично ії (аn), якщо а7= 18​...
supertriom supertriom  16.05.2021 21:14
Выполните сложение и вычитание дробей...
Alys1 Alys1  25.03.2021 16:08
Чи рівносильні рівняння: z-3=0 і 0×z=0...
Kotya005 Kotya005  25.03.2021 16:08
Пишіть те що знаєте на ці завдання​...
vankovvandam vankovvandam  25.03.2021 16:06
. Заполни таблицу: Коробке:a9716783198498b56200775173a+bа - 694Заполни таблицу-​...
alliekw3p0144w alliekw3p0144w  25.03.2021 16:00
1. укажіть функцію що є прямою пропорційністю а) у = 5х б) у = 5х - 3 в) у = 5/х г) у = х² 2. Знайдіть значення функцій х², якщо х ← 1 У = 5 - 8х, якщо х → 1...
кукипро кукипро  28.07.2019 15:20
Сократите дробь a^2-ab-bc-c^2/b^2-a^2+2ac-c^2...

Популярные вопросы