надо! пользуясь калькулятором, укажите две десятичные дроби с одним знаком после запятой, между которыми заключено число 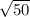$\sqrt{50}$
вычислите
упростите выражение
найдите значение выражения
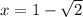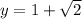
при $x = 1 - \sqrt{2}$ и $y = 1 + \sqrt{2}$

$\frac{ \sqrt{6.4} }{ \sqrt{10} }$
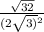
$\frac{ \sqrt{32} }{(2 \sqrt{3)} {}^{2} }$
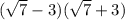
$( \sqrt{7} - 3)( \sqrt{7} + 3)$
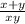
$\frac{x + y}{xy}$

Ответы

Son0905 18.01.2024 18:37

Добрый день! Давайте по порядку решим все задания.

1. Нужно найти две десятичные дроби с одним знаком после запятой, между которыми заключено число $\sqrt{50}$ .
Для начала, найдем значение числа $\sqrt{50}$ :
$\sqrt{50} = \sqrt{25 \cdot 2} = 5 \sqrt{2}$

Теперь, найдем две десятичные дроби с одним знаком после запятой, между которыми заключено число 5√2. Для этого подберем числа, которые отличаются на 0.1 и больше чем 5√2. Например:
5√2 - 0.1 = 5√2 - 0.1√2 = 5√2 - √0.2 и
5√2 + 0.1 = 5√2 + 0.1√2 = 5√2 + √0.2.

Таким образом, две десятичные дроби с одним знаком после запятой, между которыми заключено число $\sqrt{50}$ , это 5√2 - √0.2 и 5√2 + √0.2.

2. Теперь, давайте решим следующее выражение: $\frac{ \sqrt{6.4} }{ \sqrt{10} }$ .
Для упрощения этого выражения, воспользуемся свойством корня:
$\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$

Применим это свойство:
$\frac{ \sqrt{6.4} }{ \sqrt{10} } = \frac{ \sqrt{6.4} }{ \sqrt{10} } \cdot \frac{\sqrt{10}}{\sqrt{10}} = \frac{ \sqrt{6.4 \cdot 10} }{ \sqrt{10^2} } = \frac{ \sqrt{64} }{ 10 } = \frac{8}{10} = 0.8$

Таким образом, значение выражения $\frac{ \sqrt{6.4} }{ \sqrt{10} }$ равно 0.8.

3. Теперь, упростим выражение $\frac{ \sqrt{32} }{(2 \sqrt{3)} {}^{2} }$ .

Сначала, упростим знаменатель, используя свойства корня:
$(2 \sqrt{3)} {}^{2} = 2^2 \cdot (\sqrt{3})^2 = 4 \cdot 3 = 12$

Теперь, упростим числитель:
$\sqrt{32} = \sqrt{16 \cdot 2} = \sqrt{4^2 \cdot 2} = 4 \sqrt{2}$

Таким образом, значение выражения $\frac{ \sqrt{32} }{(2 \sqrt{3)} {}^{2} }$ равно $\frac{4 \sqrt{2}}{12}$ .
Для дальнейшего упрощения, можно разделить числитель и знаменатель на 4:
$\frac{ \sqrt{32} }{(2 \sqrt{3)} {}^{2} } = \frac{ \frac{4 \sqrt{2}}{4} }{ \frac{12}{4} } = \frac{ \sqrt{2} }{ 3 }$ .

Итак, упрощенное выражение равно $\frac{ \sqrt{2} }{ 3 }$ .

4. Далее, найдем значение выражения $( \sqrt{7} - 3)( \sqrt{7} + 3)$ .
Воспользуемся формулой разности квадратов: (a - b)(a + b) = a^2 - b^2

.

Применим эту формулу к нашему выражению:
$( \sqrt{7} - 3)( \sqrt{7} + 3) = (\sqrt{7})^2 - 3^2 = 7 - 9 = -2$

Таким образом, значение выражения $( \sqrt{7} - 3)( \sqrt{7} + 3)$ равно -2.

5. Наконец, найдем значение выражения $\frac{x + y}{xy}$ при $x = 1 - \sqrt{2}$ и $y = 1 + \sqrt{2}$ .

Подставим значения переменных в выражение и упростим его:
$\frac{x + y}{xy} = \frac{(1 - \sqrt{2}) + (1 + \sqrt{2})}{(1 - \sqrt{2})(1 + \sqrt{2})} = \frac{1 + 1}{1^2 - (\sqrt{2})^2} = \frac{2}{1 - 2} = -2$ .

Таким образом, значение выражения $\frac{x + y}{xy}$ при $x = 1 - \sqrt{2}$ и $y = 1 + \sqrt{2}$ равно -2.

Я надеюсь, что мои ответы и пояснения были понятны. Если у вас возникнут еще вопросы или потребуется дополнительное объяснение, пожалуйста, сообщите.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра