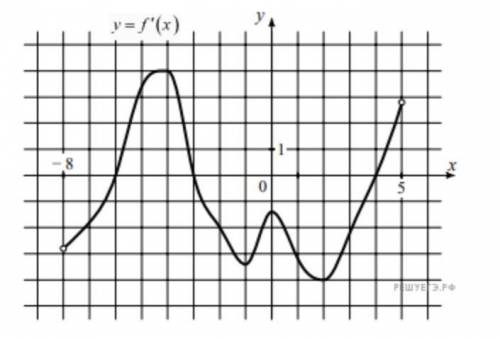
На рисунке изображён график y=f'(x) — производной функции f(x), определенной на интервале (−8; 5). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = 3x + 12 или совпадает с ней. Подробно
Другие вопросы по теме Алгебра
Популярные вопросы
- укажи слова приставкой при- а)пр...милый б)пр...града в)пр...вязал...
2 - Ребят география 7 класс заполнить небольшую таблицу...
3 - Какую окраску шерсти имеет гималайский кролик при обычных комнатных...
2 - все три задание.Первое задание выбрать живое или неживое.Второе не...
2 - -19/(х+5)^2-6= 0 с решением...
3 - В гипоталамусе находятся центры: нейрогуморальной регуляции ориентировочных...
3 - 1. Сравнить что больше? ( при вычислении использовать свойства вычитания...
2 - 1. Fill in the words from the box to make up word com- binations cup...
2 - ОЧЕНЬ 1. Where are deserts found? A. Africa and South America B. The...
1 - Доказать методом математической индукции если не понятно что написано1^3+2^3+3^3...+...
2
Объяснение:
прямая параллельна прямой y = 3x + 12 или совпадает с ней если ее угловой коэффициент равен 3
угловой коэффициент касательной к графику функции равен значению производной в точке касания
то есть f'(x)=3
На графике производной есть две точки у которых ордината =3
это А и В
ответ две