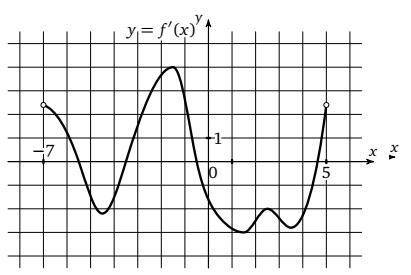
На рисунке изображен график производной функции f(x), определенной на интервале (-7;5). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-6;-1].
Популярные вопросы
- Составить формулы солей: А) Нитрат железа (II) -Б) Сульфат алюминия –В)...
1 - Ким працює Андрій Шишига? 4. Що означає прізвище головного героя? 5. Від...
1 - Крч я не так написал 100:(3×-1)=4...
2 - Твір даруйте дива своїм близьким за новелою Дари волхвів 1,5-2 сторінки...
2 - Укажи речення зі звертанням А моя думка - краще закріпитися і чекати до...
1 - 1 глагол во всех наклонениях азербайджанский язык ...
3 - ДАМ Скільки сягає око усе навколо вкрите кригою. Часом ця крижана пус-теля...
3 - Якими були політичні й соціальні наслідки Війни за незалежність для США...
1 - Марию Никифоровну портерт...
1 - Поясніть відмінність в кількості опадів на південно-західних схилах Кримських...
3
ответ: одна точка.
Объяснение:
Максимум функция может иметь только в тех точках, в которых её производная обращается в ноль. На отрезке [6;-1] таких точек две: x=-5,5 и x=-3,5. При переходе через точку x=-5,5 производная меняет знак с + на - , поэтому эта точка является точкой максимума. При переходе через точку x=-3,5 производная меняет знак с - на + , поэтому эта точка является точкой минимума.