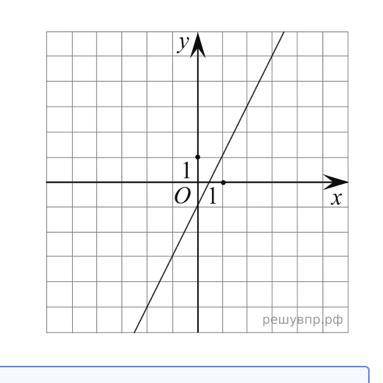
На рисунке изображён график линейной функции. Напишите формулу, которая задаёт эту линейную функцию

Начнем с определения линейной функции. Линейная функция - это функция вида f(x) = mx + b, где m - наклон прямой (тангенс угла наклона), а b - точка пересечения с осью ординат, или угловой коэффициент и свободный член.

Чтобы найти уравнение линейной функции, нам нужно знать две точки на графике, чтобы определить наклон и свободный член.

Давайте рассмотрим график, представленный на изображении.

У нас есть две определенные точки на графике: точка A (2, 7) и точка B (4, 11). Мы можем использовать эти точки для нахождения уравнения.

Шаг 1: Найдем наклон (m) прямой, используя формулу наклона:

m = (y2 - y1) / (x2 - x1)

где (x1, y1) и (x2, y2) - координаты двух точек.

Заменим координаты точек A (2, 7) и B (4, 11) в формуле:

m = (11 - 7) / (4 - 2) = 4 / 2 = 2.

Таким образом, наклон (м) равен 2.

Шаг 2: Теперь найдем свободный член (b), используя одну из заданных точек и найденный наклон. Мы можем использовать точку A (2, 7) и наклон m = 2 для нахождения b.

Используем формулу:

y = mx + b.

Заменим координаты точки A (2, 7) и найденный наклон m = 2 в формулу:

7 = 2 * 2 + b.

7 = 4 + b.

b = 7 - 4.

b = 3.

Таким образом, свободный член (b) равен 3.

Шаг 3: Подставляем найденные значения наклона и свободного члена в уравнение линейной функции:

f(x) = mx + b.

f(x) = 2x + 3.

Таким образом, формула, которая задает эту линейную функцию, будет f(x) = 2x + 3.