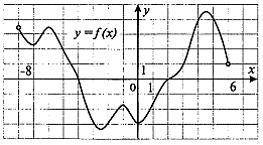
На рисунке изображен график функции y = f(x), определенной на интервале (- 8; 6). Определите количество целых точек, в которых функция возрастает.

Для определения количества целых точек, в которых функция возрастает на данном графике, мы должны понимать, что функция возрастает в тех точках, где значение функции увеличивается по мере увеличения значения x.

На графике мы видим, что функция y = f(x) начинается с отметки -2 и увеличивается до отметки 4. Это означает, что функция возрастает на промежутке от x = -8 до x = 6.

Чтобы определить количество целых точек, в которых функция возрастает, мы можем просмотреть каждое целое значение x в этом промежутке и проверить, увеличивается ли значение функции в этой точке.

Если мы рассмотрим каждое целое значение x от -8 до 6, мы обнаружим, что функция возрастает на каждом из этих значениях. Таким образом, количество целых точек, в которых функция возрастает, равно разности первого и последнего значения x (6 - (-8)) плюс 1, так как первое и последнее значение также включены.

Итак, количество целых точек, в которых функция возрастает, равно 6 - (-8) + 1 = 15.

Таким образом, на данном графике функция возрастает в 15 целых точках.