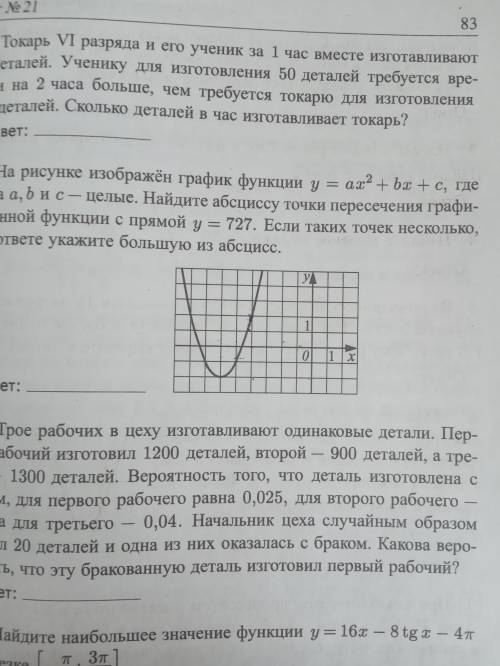
На рисунке изображен график функции y=ax^2+bx+c, где числа a,b и с - целые. Найдите абсциссу точки пересечения графика данной функции с прямой y=727. Если таких точек несколько, то в ответе укажите большую из абсцисс.
Другие вопросы по теме Алгебра
Популярные вопросы
- Сочинение на тему человек часть природы...
2 - Придумать текст с водными словами всех значений ?...
2 - Вопросы сложные с ответами к рассказу дубровский 3 штуки...
3 - Определи склонение и падеж имен существительных/ масло,село,седло,крыло,сено,добро...
3 - Сделать синтаксический разбор предложения. мама купила вкусный торт к чаю....
2 - Вкаких странах кроме россии использованы идеи кулибина...
1 - Отметить биссектрисы, медианы и высоты тупоугольного треугольника....
3 - Какой путь развития должна выбрать россия по мнению чаадаева...
3 - 1.рассчитайте относительные молекулярные массы веществ по формулам а)h2so3...
3 - Какие цветы растут весной,летом и осеньюнапиши их....
2
Пересечение графика функции и прямой означает, что значения y на графике функции и на прямой равны в данной точке. То есть у нас есть следующее уравнение:
ax^2 + bx + c = 727
Для решения этого уравнения, нам необходимо найти значения x, при которых это уравнение выполняется.
Шаг 1: Подставляем значение y=727 в уравнение
ax^2 + bx + c = 727
Шаг 2: Переносим 727 на другую сторону уравнения
ax^2 + bx + c - 727 = 0
Шаг 3: Приводим уравнение к каноническому виду
ax^2 + bx + (c - 727) = 0
Шаг 4: Решаем уравнение квадратного типа, используя формулу дискриминанта
Для уравнения вида ax^2 + bx + c = 0, дискриминант D вычисляется по формуле D = b^2 - 4ac.
Если D > 0, то есть у уравнения есть два корня.
Если D = 0, то есть у уравнения есть один корень.
Если D < 0, то есть у уравнения нет корней.
Шаг 5: Вычисляем дискриминант
D = b^2 - 4ac
В данном случае у нас a = 3, b = -9 и c = 731, поэтому
D = (-9)^2 - 4 * 3 * (731 - 727)
= 81 - 4 * 3 * 4
= 81 - 48
= 33
Шаг 6: Анализируем значение дискриминанта
Так как D > 0, у уравнения есть два корня.
Шаг 7: Используем формулу корней квадратного уравнения
x = (-b ± √D) / (2a)
Подставляем значения a = 3, b = -9, c = 731 и D = 33 в формулу
x = (-(-9) ± √33) / (2 * 3)
= (9 ± √33) / 6
Теперь у нас есть два значения x, и нужно выбрать большее из них.
x1 = (9 + √33) / 6
x2 = (9 - √33) / 6
Шаг 8: Вычисляем абсциссу точки пересечения
Так как нам нужно указать большую из абсцисс, выбираем x1.
x1 = (9 + √33) / 6
Ответ: Абсцисса точки пересечения графика функции с прямой y=727 равна (9 + √33) / 6.