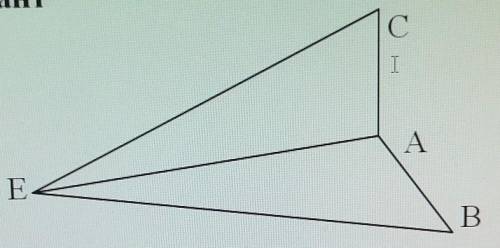
На рисунке EA - биссектриса LCEB, EC = ЕВ.
Доказать: LC — LВ.​

Для доказательства, что LC и LB являются поворотно-симметричными лучами, мы можем использовать свойства биссектрисы и доказать, что углы между лучами и отрезком EB равны.

Шаг 1: Используя определение биссектрисы, угол LCE равен углу ECB, а угол BCE равен углу ECA.

Шаг 2: Мы знаем, что EC равно EB, как дано в условии. Значит, треугольники ECA и ECB равнобедренные, так как у них равны основания и две стороны.

Шаг 3: Теперь, используя свойство равнобедренных треугольников, мы можем сделать вывод, что углы ACE и BCE равны.

Шаг 4: Поскольку углы ACE и BCE равны, то и углы ECA и ECB также равны. То есть, углы LCE и ECB равны.

Шаг 5: Наконец, мы можем сделать вывод, что луч LC и луч LB являются поворотно-симметричными лучами, так как они имеют равные углы с отрезком EB.

Таким образом, мы доказали, что LC и LB являются поворотно-симметричными лучами.