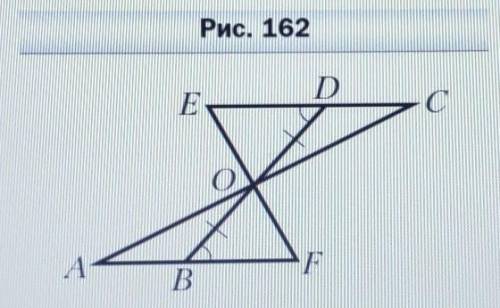
На рисунке 162 DO = OB, ∠EDO = ∠OBF. Докажите, что СОЕ = AOF.
Ответы
Чтобы доказать, что СОЕ = AOF, мы должны использовать имеющиеся условия на рисунке и применить соответствующие геометрические теории и свойства.
Итак, у нас есть следующие данные:
- DO = OB (условие на рисунке)
- ∠EDO = ∠OBF (условие на рисунке)
Нам нужно найти СОЕ и AOF, чтобы сравнить их.
Шаг 1: Рассмотрим треугольники СОЕ и AOF.
Шаг 2: Поскольку DO = OB, мы можем сказать, что отрезок DE равен отрезку AF (потому что AD = DB, а EF - продолжение AD и AF).
Шаг 3: Затем мы обращаемся к условию ∠EDO = ∠OBF. Это означает, что угол EDO равен углу OBF.
Шаг 4: Теперь, если мы сравним треугольники СОЕ и AOF, мы увидим, что у них есть одинаковые стороны (отрезки DE и AF), а также одинаковый угол (угол EDO = угол OBF).
Шаг 5: Согласно теории подобных треугольников, если у двух треугольников есть одна пара равных углов и одна пара пропорциональных сторон, то они подобны.
Шаг 6: Из этого следует, что треугольники СОЕ и AOF подобны.
Шаг 7: Поскольку они подобны, соответствующие углы в них будут равны. То есть СОЕ = AOF.
Таким образом, мы доказали, что СОЕ = AOF, используя имеющиеся условия и геометрические теории.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Популярные вопросы
- Списать предложения. Расставить знаки препинания. Волк линя...т а...
1 - Образи п єси блакитний птах можна умовно розподілити на три групи...
2 - У Фермерському господарстві під гречку відведено 19 га причому гречка...
3 - Яким було духовне життя давніх слов ян...
1 - Написать программу, которая вычисляет частное двух чисел. Программа...
1 - ⦁ Что явилось причиной появления разных признаков у лебедей? Объясните...
2 - Описание Италии по плану: 1. Географическое положение. Регион. Страны...
2 - Сколько единичных кубов объемом 1 см³ нужно взять, чтобы построить...
3 - Прочитайте слова Объясните их значение Составьте словосочетания или...
3 - с арифметической прогрессией....
1