1. Алгебра
  2. На примере 3sin²x-4sinx·cosx+cos²x=0

На примере 3sin²x-4sinx·cosx+cos²x=0 объясните один из видов решения тригонометрического уравнения.

sndzhychayana sndzhychayana    1   03.06.2019 22:00    0

Ответы
vigura2 vigura2  01.10.2020 18:51
 Заметим то что 
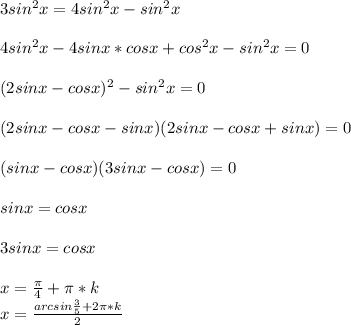
 3sin^2x=4sin^2x-sin^2x\\\\
 4sin^2x-4sinx*cosx+cos^2x-sin^2x=0\\\\
 (2sinx-cosx)^2-sin^2x=0\\\\
 (2sinx-cosx-sinx)(2sinx-cosx+sinx)=0\\\\
 (sinx-cosx)(3sinx-cosx)=0\\\\
 sinx=cosx\\\\
 3sinx=cosx\\\\
 x=\frac{\pi}{4}+\pi*k\\
 x=\frac{arcsin\frac{3}{5}+2\pi*k}{2}
ПОКАЗАТЬ ОТВЕТЫ
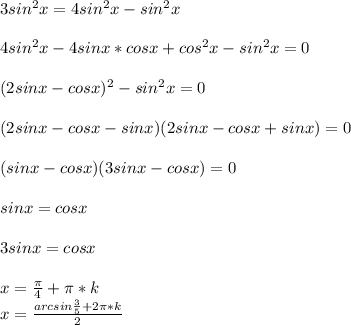
Другие вопросы по теме Алгебра
МаринаДоблер МаринаДоблер  20.08.2019 14:50
Разложите на множетили многочлен 3xy-xy^2+2y-6...
ахаххахаха11 ахаххахаха11  20.08.2019 14:50
Найдите неизвестный член пропорции x: 1 целая 3/7=1 целая 1/5 : 1 целая 1/3...
геля217 геля217  20.08.2019 14:50
Из дома в школу оля вышла на 5 минут позже гоша, но шла в два раза быстрее, чем он. через сколько минут после своего выхода оля догонит гошу?...
artem759342 artem759342  20.08.2019 14:50
Выражение и найдите его значение при указанных значениях переменной. (5+2x)^2-2.5x(8x+7) при x=-0.5...
bogdankpro bogdankpro  20.08.2019 14:50
Вычислите: log(2) x^5 если log(2) x=1,2...
87348732 87348732  21.04.2020 10:18
Y= 2x3-9x2+12x-9 Дослідити функції та побудувати графік...
Света3811 Света3811  21.04.2020 10:18
Найди значение выражения √64*√625...
The0ruyman The0ruyman  21.04.2020 10:18
У выражение (3 –а )(3 +а) (9 +а2) + (4 +а2)2 и найти его значение при а =1/2 ....
Guguguguguguguguy Guguguguguguguguy  30.03.2019 06:10
Логарифм х по основанию 2 меньше 1/2 решить...
Dalishka808 Dalishka808  30.03.2019 06:10
Найдите tg альфа, если tg (альфа + пи/4) =4...

Популярные вопросы