На п'яти картках записані числа 2,4,6,7,8. Навмання обирають дві картки і складають правильний дріб. знайти ймовірність того що даний дріб нескоротний
Другие вопросы по теме Алгебра
Популярные вопросы
- 1274⁹записать число в пятиричной системе...
1 - Объясните на примере одной из картин цикла о Марии Медичи (Рождение...
3 - тему пропустил. Дана арифметическая прогрессия: −19; −15; −11......
2 - Допишите недостающие обозначения...
2 - В мае 2012 цена такси в Бишкеке увеличивалась на 8-10 сом. На сколько...
3 - 1)(25b²-10b+1) :10b²-2b/4b; 2)(х+2)²-1=x(x-1)-(x-3)(x+3); 3)y²-9/2y²-4y-6;...
3 - Как ты считаешь, соответствует ли этот документ идеям революции !...
2 - Ознака яка не сприяла освоєнню суходолу комахами цеА)хитиновий покрытаб)невеликі...
2 - Что объединяет две новеллы Ги Де Мопасана « Пышка» и «Мадмузель фифи»...
1 - Выбери ряд слов, в котором есть лишний глагол. Выпиши его и определи,...
3
Объяснение:
Якщо чисельник менший від знаменника, то такий дріб називається правильним. Усього таких правильних дробів буде 10, перерахуємо їх:
Побачимо, що всього скоротних дробів є рівно 6, а не скоротних - відповідно, 4. Питається: яка ймовірність отримати нескоротний дріб із 10?
Обчислимо цю ймовірність за класичною формулою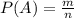 , де A - подія; P(A) - ймовірність цієї події; n - загальна кількість подій (10), а m - число подій, які сприяють події A (4). Маємо:
, де A - подія; P(A) - ймовірність цієї події; n - загальна кількість подій (10), а m - число подій, які сприяють події A (4). Маємо: