На максимум и минимум : число 54 представьте в виде суммы трех положительных чисел так,чтобы отношение первого числа ко второму было равно 3: 1, а произведение всех трех чисел была наибольшим.
Другие вопросы по теме Алгебра
Популярные вопросы
- Япредпочитаю ходить за покупками в (large shoping centres),я редко покупаю...
3 - Используя линейку без делений, постройте на листе а4 квадрат со стороной...
2 - Автобус проходит расстояние между двумя пунктами, равное 36 км, за 40...
1 - Выткался на озере алый свет зари наоборот со звонами плачут глухари что...
3 - Придумайте оригинальную тему (можно несколько) для проекта 11 класса по...
1 - Причины, предпосылки и условия столыпинских реформ в россии. программа...
1 - Составить сообщение (по родному языку) по теме: диалектизмы использование...
1 - Какие условия называются основными для фотосинтеза...
1 - Какой монастырь в период смутного времени начала xvii в. успешно выдержал...
3 - Что говориться о смерти остапа в повести тарас бульба ?...
2
Пусть первое число равно 3а,тогда второе равно а,третье число равно b
Тогда имеет место система:
По условию функция вида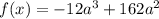
Должна принимать максимальное значение на области определения:
Рассмотрим эту функцию:
Очевидно,что она принмает положительные значения на интервале:
В точке,где функция принимает максимальное значения касательная к функции есть константа вида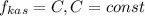
То есть тангенс угла наклона касательной равен нулю:
Первая точка не подходит по условию задачи,значит
а=9,3a=27,b=54-4*9=18