На комплексной плоскости даны точки z1=6+8i, z2=4-3i. найдите комплексные числа, соответствующие точкам, лежащим на биссектрисе угла, образованного векторами z1 и z2
Другие вопросы по теме Алгебра
Популярные вопросы
- Скакой целью используются в речи слова с переносным значением и синонимы ?...
2 - Вкакую отрасль вы бы вложили свой капитал в казахстане? и в какой области? в...
2 - Какими могут быть социальные роли? как они соотносятся?...
1 - Умаши 7 кукол, а у ани 13 кукол . во сколько раз у ани больше кукол, чем у маши?...
3 - Выбери число при делении которого на 100 получается наибольший остаток...
3 - Заполни пропуски а+8 сумма. 100- и х 46+с-- и с...
1 - Какой из видов полностью подавляет при совместном выращивании, как быстро это...
3 - Расстояние между двумя машиначи движущимися по шоссе 100км скорости машин 80...
1 - Какое значение имела куликовская битва для . назовите памятники и произведения...
1 - Вкорзине лежит 15 красных яблок, что составляет 3/5 всех яблок. сколько всего...
3
Как и в предыдущей твоей задаче, комплексное число a+bi можно рассматривать как вектор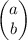 . Как видно из сложения векторов по правилу параллелограмма, сумма двух векторов, имеющих общее начало, является диагональю параллелограмма, двумя сторонами которого являются начальные векторы. Диагональ параллелограмма — это биссектриса его угла. Значит, конец любого вектора, лежащего на луче, продолжающем диагональ параллелограмма, подходит для ответа.
. Как видно из сложения векторов по правилу параллелограмма, сумма двух векторов, имеющих общее начало, является диагональю параллелограмма, двумя сторонами которого являются начальные векторы. Диагональ параллелограмма — это биссектриса его угла. Значит, конец любого вектора, лежащего на луче, продолжающем диагональ параллелограмма, подходит для ответа.
d = 6+8i + 4-3i = 10 + 5i
Вектор v, соответствующий d — (10; 5). Любая точка (n;m) такая, что существует такое неотрицательное число k такое, что k*d = (n;m), лежит на биссектрисе.
Таким образом, n/m = 10/5 = 2.
ответ: {(n+mi) | n/m = 2}