Алгебра: На фото. найдите произведение корней уравнения

На фото.
найдите произведение корней уравнения

Ответы

melnicoff 05.10.2020 19:03

Задачка может казаться сложной, на самом деле это не так.

Знаки сумм писать не буду, просто распишу:

(x^2+x^2+...+x^2)+(-x+0+x+2x+...+10x)+(1+2+...+12)=234

Имеют место быть арифметические прогрессии для каждого из коэффициентов квадратного уравнения.

n=12, это видно (1...12).

С 1-ым коэффициентом совсем легко, 1+1+..+1=12

Считаем 2-ой: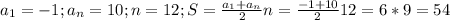 $a_1=-1; a_n=10; n=12; S=\frac{a_1+a_n}{2}n=\frac{-1+10}{2}12=6*9=54$

Считаем 3-ий: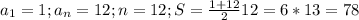 $a_1=1; a_n=12; n=12; S=\frac{1+12}{2}12=6*13=78$

Имеем теперь:

12x^2+54x+78-234=0; 12x^2+54x-156=0; 2x^2-9x-26=0;

Произведение корней по теореме Виета:

$x_1x_2=\frac{c}{a}=\frac{-26}{2} =-13$

ответ: -13

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

tokio3 14.06.2019 19:50

ketrinkryt 14.06.2019 19:50

suorevc 14.06.2019 19:50

VeshkinRuslan 14.06.2019 19:50

Найдите значение выражения 2ас при а= и с=...

угуртунджай 14.06.2019 19:50

Вычислить: 1) ∛20+14√2+ ∛20-14√2 2) ∛5√2+7+ ∛5√2-7 : √57+12√15 )...

Zarina2206 14.06.2019 19:50

BelkinaDasha000 14.06.2019 19:50

Решить систему неравенств: {8-2x≥2 {4x-5≥-3/...

student130 14.06.2019 19:50

Анасія 16.06.2019 21:20

daudovam17 16.06.2019 21:20