Можно с подробным решением.
Другие вопросы по теме Алгебра
Популярные вопросы
- Что значит эти ворожения? вороной конь - спелая рожь - скорый на работу...
3 - Площадь боковой поверхности цилиндра равна 30π. найдите площадь сечения...
1 - Как разобрать слово наш под цифрой 3...
2 - ((4: 0,128+14628,25): 1,011*0,00008+6,84): 12,5= плз...
3 - Сделать (+ i often (to swim) . i (to swim) now. she (to like) music...
3 - Плоды томатов бывают грушевидные и круглые , круглая форма доминант. какими...
3 - Где предлог, а где приставка? по (по)слышалось, (по)квартире, (по)крышка,(по)крыше....
3 - 3. для того чтобы наполнить вареньем 8 банок,потребовалось 960г варенья.сколько...
3 - 2.)как выполняется питание: компьютерных мышей проводных и без проводных...
2 - Составить предложение из нескольких слов весна наступает снег тает лед потемнел...
3
а) Если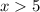 , то
, то 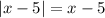 , тогда
, тогда 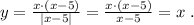
б) Если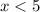 , то
, то 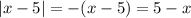 , тогда
, тогда
Строим две прямые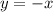 на промежутке
на промежутке 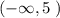 и
и 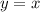 на промежутке
на промежутке 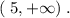
График нарисован сплошными линиями .