Можно решение на листочке
и формулы,которые вы использовали
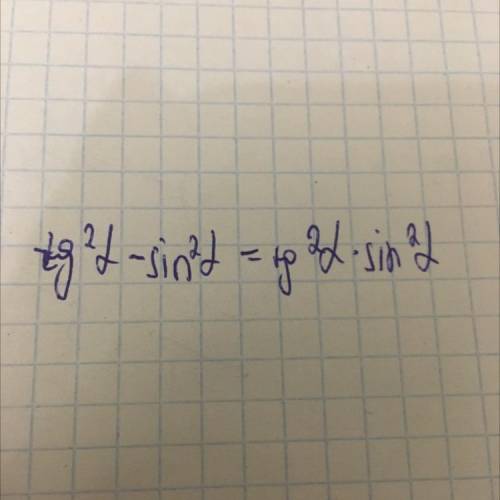
Другие вопросы по теме Алгебра
Популярные вопросы
- Бассейн емкостью 3500 л наполняют водой из двух труб.одна из труб наполнила 1/7...
2 - Написать доклад о том как строили санкт-петербург...
3 - Укажите грамматически правильное продолжение предложение. находясь в пути, 1.нам...
2 - От друзей приходили письма, зовущие к твёрдости и продолжение борьбы. синтаксический...
1 - На складе было 567 мешков с сахаром. один магазин взял 2/7 этого количества,...
3 - Вполдень по сравнению с утром температура воздуха изменилась на плюс 2 к вечеру...
3 - Нпишется в слове: а) закон..ый б) деревя..ый в) гости..ый двор г) правительстве..ый...
2 - Первый учёный предположивший что вселенная бесконечна...
1 - Вчем различие окончаний глаголов 1 и 2 спряжения...
2 - Как найти корень уравнения 3 в степени х =27...
3
Доказать триг. тождество.