Можете с каким либо из этих Дифф.Уравнениями? Буду благодарен за все
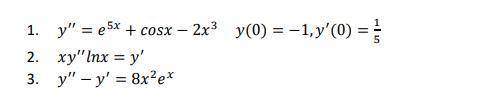
Другие вопросы по теме Алгебра
Популярные вопросы
- 5. Составьте текст из 4-5 предложений, описав дальнейшие приключения...
2 - В чем особенность существительных общего рода? ...
3 - Почему возникает электромагнитная сила ?...
3 - Берілген аинымалыларды берілген типтерімен сёикестендір ИНФОРМАТИКА...
2 - https://sun9-34.userapi.com/impg/mluryCqvyWvFT-_W0JVWWh9TOrEW0o3D_Ca7pg/wVxoeWCPSW4.jpg?size=960x1280&quality=96&sign=76688db213069febbe02520557b86bf6&type=album...
1 - Иван Грозный в романе Князь серебряный...
1 - ДУЖЕ ТРЕБА ІТЬ БУДЬ ЛАСКА ІВ Розвязати задачу При взаємодії насиченого...
1 - Task 3. Complete the sentences using: a matter of time, beat...
2 - Напишите названия цифр на картинке....
3 - У прямокутному трикутнику АХК Х = 90°, АС – бісектриса трикутника,...
1
1) Интегрируем обе части: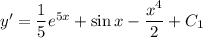 . Поскольку
. Поскольку 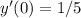 , то
, то 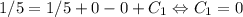 . Интегрируем еще раз:
. Интегрируем еще раз: 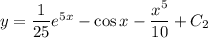 . Но поскольку
. Но поскольку 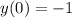 , то
, то 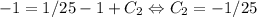 . Следовательно, ответ:
. Следовательно, ответ: 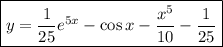
2) Сделаем замену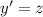 . Тогда
. Тогда 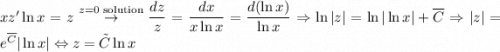
После обратной замены: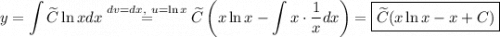
3) Здесь снова делаем замену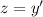 . Тогда
. Тогда 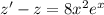 . Решаем однородное уравнение:
. Решаем однородное уравнение: 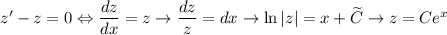 . Применяем метод вариации постоянной, то есть ищем решение в виде
. Применяем метод вариации постоянной, то есть ищем решение в виде 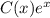 :
: 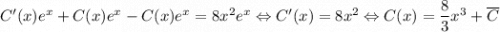 . Значит,
. Значит, 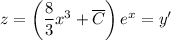 . Здесь просто интегрируем. Чтобы не делать несколько раз интегрирование по частям, можно понять, что первообразная
. Здесь просто интегрируем. Чтобы не делать несколько раз интегрирование по частям, можно понять, что первообразная 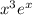 имеет вид
имеет вид 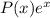 , где
, где 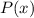 -- некоторый полином. Тогда
-- некоторый полином. Тогда 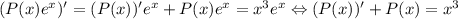 , то есть по сути, требуется решить еще один диффур, но можно поступить проще:
, то есть по сути, требуется решить еще один диффур, но можно поступить проще: 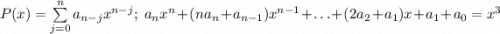 , откуда
, откуда 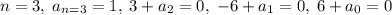 , следовательно,
, следовательно, 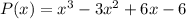 . Имеем:
. Имеем: 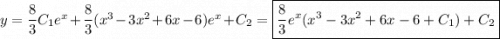 , где
, где  .
.