Можете написать ответ с решениями
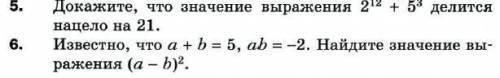
Другие вопросы по теме Алгебра
Популярные вопросы
- Определите стоимость земельного участка методом выделения, если известно, что недавно...
1 - Расставь числа от одиннадцати до 17 включительно так-то Сумма чисел в каждой из...
1 - Оценить основные фонды автосервисного предприятия в стоимостном выражение на начало,...
1 - Проверь, верно ли равенство, используя основное свойство пропорции: 1,5\4=3\8. ответ:...
3 - 1. Как найти длину отрезка, заданного координатами концов? Запиши формулу 2. Как...
3 - Найдите сумму многочленов (3x^5 – х + 4) и ( х^3+ 2х алгебра...
1 - Https://www.youtubeind.com/user.php?u=tyjon https://www.youtubeind.com/watch.php?vid=285fcf2af...
2 - Определи порядок действий и найди значения выражений...
2 - Найти глагол в будущем времени буду смотреть ,летит , сварили ,пишет ?...
3 - Укажите группу, в которой Есть слово (словосочетание), которое может быть как водные...
1
Объяснение:
Номер 6
(a - b)^2 = a^2 - 2ab + b^2
(a + b)^2 = a^2 + 2ab + b^2 =>
=> (a - b)^2 = (a + b)^2 - 4ab = 5^2 - 4 * (-2) = 25 + 4 * 2 = 33
Номер 5
2^6, 2^12 и так до 2^(6*n) имеет остаток от деления на 21 равный 1
5^3 = 125, посчитать не сложно
125 имеет остаток 20 от деления на 21
чтобы сумма чисел делилась на m, сумма их остатков должна делиться на m => чтобы 2^12 + 5^3 были кратны 21, их остатки должны суммарно давать число кратное 21
20 + 1 = 21
21 : 21 = 1 => сумма остатков кратна 21 => сумма чисел кратна 21