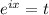Может ли у тригонометрического уравнения быть комплексные корни?
Другие вопросы по теме Алгебра
Популярные вопросы
- Підготувати національний твір про гімн україни...
3 - Iv. перепишите и письменно переведите 2, 3 и 4-й абзацы текста. the...
2 - Как разделить прямоугольник 5 на 3 см на 5 разных прямоугольников?...
2 - Что такое инфляция и преодоления?...
3 - Слово к транскрипции [0i: m pa: k] [iks k3: |an] [ tre3a]...
2 - Почему некоторые права являются и гражданскими, и политическими?...
3 - Отсортируйте величины в порядке убывания в ответе запишите комбинацию...
3 - Решить это уравнение 3(x-1.1)+4(12x+2)=7.3x+0.7...
1 - Известно,что кр= ре= ef= ft = 2см. какие...
2 - Установить соответствие 8 бит 1024 байт 2 кбайт и 2048 кбайт 2 мбайт...
1
Да, приведу самый простой пример:
Очевидно, что действительных решений тут нет.
Попробуем найти комплексные:
Сделаем замену :