Моторная лодка проплыла 9 км по течению реки и 14 км против течения за такое же время, которое понадобится ей, чтобы проплыть 24 км в стоячей воде. найдите скорость лодки в стоячей воде, если скорость течения составляет 3 км/ч.

ответ: 24 км/ч.

Объяснение: Пусть х км/ч скорость лодки в стоячей воде, тогда скорость лодки по течению реки х+3 км/ч, а против течения х-3 км/ч. Времени по течению реки, на расстояние в 9 км, лодка затратила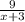 часов и против течения реки, на расстояние в 14 км, лодки затратила 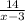часов, что в сумме будет равно времени затраченным на расстояние в 24 км, в стоячей воде, это 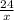часов. Составим уравнение:

x₁=(-9) км/ч не подходит, т.к. скорость не может быть отрицательной.

x₂=24 (км/ч) скорость лодки в стоячей воде.