Мотоциклист предполагал проехать расстояние 90 км за определенное время. проехав 54 км, он должен был остановиться у закрытого шлагбаума на 5 мин. продолжив движение, он увеличил скорость на 6 км/ч и прибыл к месту назначения в намеченное время. найдите первоначальную скорость мотоциклиста.
Другие вопросы по теме Алгебра
Популярные вопросы
- На весах уравновешаны 2 одинак тела 1 и 2.изменится ли равновесие ,если...
1 - 1.один брат — ест и голодает, а другой — идёт и пропадает.2.змея разлеглась...
2 - Составьте вопросы по окружающему миру с ответами 2 часть плешаков до...
1 - Выполни действия 6 мин 40 сек + 34 сек = сек 5 мин 30 сек ÷ 90 сек =...
2 - Українське національне відродження котляревський енеїда...
2 - Запишите по три слова с префиксами на з с чтобы в них на стыке префикса...
1 - Найдите ошибки в тексте и исправьте их. 1)дыхание подчиняется нервной...
3 - Произведениям декоративно-прикладного искусства свойственно: функциональное...
1 - Срешением уравнений, ! само решение необходимо. решите уравнения, найдите...
3 - 3÷1-x+1x+1=28÷1-x^2розв язати рівняння...
1
Пусть (км/ч) - первоначальная скорость мотоциклиста.
(км/ч) - первоначальная скорость мотоциклиста.
Тогда время, за которое он преодолел путь в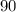 километров, равно
километров, равно 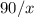 часов.
часов.
Но, с другой стороны, сумма трех других отрезков времени равна тому же промежутку времени (по условию). Это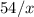 часов,
часов, 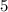 минут или же
минут или же 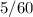 часа =
часа = 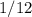 часа. И последний промежуток,
часа. И последний промежуток, 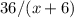 часов (
часов (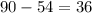 километров со скоростью
километров со скоростью 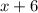 км/ч).
км/ч).
Теперь, конечно, будем решать уравнение:
Получилось два корня. Второй доверия не внушает из-за своей отрицательности, так что возьмем исключительно первый.
Первоначальная скорость мотоциклиста -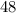 км/ч.
км/ч.
Задача решена!
ответ: 48 км / ч .