Могут ли четыре числа, представляющие три стороны, и начальное число треугольника образовать арифметическую прогрессию?

Ответы

неведимка17108 20.06.2021 17:38

ответ: нет .

Пусть стороны треугольника равны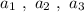 $a_1\ ,\ a_2\ ,\ a_3$ , а периметр

P=a_1+a_2+a_3 .

Если они образуют арифметическую прогрессию, то тогда выполняется:

$a_1=a\\a_2=a+d\\a_3=a+2d\\P=a+3d\\\\P=a+(a+d)+(a+2d)=3a+3d\ \ ,\ \ \ 3a+3d=a+3d\ \ \ \Rightarrow \\\\3a=a\ \ ,\ \ 2a=0\ \ ,\ \ a=0$

Сторона треугольника не может равняться 0 .

Поэтому не существуют 4 числа, являющиеся сторонами треугольника и его периметром, образующих арифметическую прогрессию .

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

pchehov77 13.09.2019 17:20

tatiana158 13.09.2019 17:20

vladssos04 13.09.2019 17:20

ьапттыт 13.09.2019 17:20

sidorova123441 13.09.2019 17:20

KIrito5016 23.08.2019 19:00

ЗалияАлиматова 23.08.2019 19:00

FedushkinDmitry95 23.08.2019 19:00

Постройте прямую заданную уравнением г)y=-0,5x е)y=-x/4...

Морти111 23.08.2019 19:00

svetlana50036 08.04.2020 10:45

Тупо маленький тест, решите умоляю...

Могут ли четыре числа, представляющие три стороны, и начальное число треугольника образовать арифметическую прогрессию?​