Множество решений неравенства log0,8 (2х-4)/(8-х)> =0 имеет вид
Другие вопросы по теме Алгебра
Популярные вопросы
- 220%перевести в обыкновенную дробь...
2 - Виконайте завдання клоуз-тестів 1. З вертанням називають слово в...
1 - При зміні довжини хвилі падаючого випромінювання від 200 до 300...
2 - Які проблеми людського життя порушує автор у вірші Листівки з видами...
3 - Как изменился облик Москвы и Санкт- Петербурга в XIX веке?...
2 - У выражение и вычислите его : 1/3+7/24−1/8, если =1/12....
1 - Третья зима его жизни приходила к концу. На дворе уже таял снег,...
2 - які зусилля потрібно прикласти щоб утримати під водою бетонний блок...
2 - пожаоуйста , физика 11 клас кр...
1 - Запишите число, в котором 8 единиц 11 класса. Уменьшите его в 20...
2
f(t) =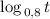 - убывает на всей области определения t∈(0;+∞).
- убывает на всей области определения t∈(0;+∞).
Решение неравенств из системы методом интервалов и решение самой системы в приложенном файле.
ответ: (2;4].