Много каковы координаты вершины параболы y=k(x+a)^2+b
Другие вопросы по теме Алгебра
Популярные вопросы
- Все работы хороши, выбирай от души! Составление словосочетаний, предложений...
3 - 《Алтын адам 》 туралы əңгіме құрастыру мне это надо отправить ...
1 - Xo jaligi, fanida oila haqida gapirilgailuaTeTO1. Davlat musiqa maktabi...
1 - Установить хронологичну послиловнисть подий...
2 - БИОХИМИЯ! Компонент F0 является: Гидрофильным Гидрофобным Амфифильным...
1 - Закончите предложения. Поставьте глаголы в времени...
3 - Книги стали дороже, тиражи стали меньше - примерно как в XIXвеке. Почему...
3 - Функция задано формулою f(x) =x2-5x...
2 - №1 Ледник длиною 1км и шириной 0,5 метра заполнен слоем льда, толщиной...
3 - Дайте определение профессии «ПЛОТНИК»...
3
ответ: (-а;b)
Объяснение:
ответ: (-a; b)
Объяснение: Докажем, что (-а; b) - координаты данной параболы.
Пусть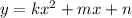 , где k не равняется 0.
, где k не равняется 0.
У первых двух слагаемых k вынесем за скобки: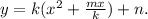 .
.
В скобках выделим полный квадрат:
Сделаем замены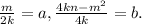
Заметим, что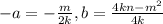 и есть формулы для определения координат вершины параболы
и есть формулы для определения координат вершины параболы 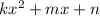 . Т.е. абсцисса у нас -а, ордината - b.
. Т.е. абсцисса у нас -а, ордината - b.