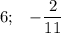Мне нужно решение уравнения через дискриминант с подробным решением и объяснением.
Другие вопросы по теме Алгебра
Популярные вопросы
- Боковое ребро правильной четырехугольной пирамиды наклонено к плоскости основания...
1 - 23,,6+8,4)+(-4,7-1)= раскройте скобки и найдите значение выражения. распишите...
3 - 1. придумать свою политическую партию (название) 2. структура 3.за что отвечает...
2 - Решить уравнение. 4х – 2,55 = -2х + 1, 05...
2 - Прачытайце. пастаўце дзеясловы часе. з далёкага краю (прыляцець) ластаўка....
2 - Найти объем комнаты если длина 5 см ширина на 1,64 меньше длины а высота в...
1 - Спиши.выбери слова с противоположным значением. зимой заяц беленький ,а летом...
3 - Почему василия шуйского прозвали «боярским царём»?...
1 - Мини-сочинение знаменитые люди афин...
3 - Расставьте знаки препинания.подчеркните обособления как члены предложения....
1
Корни уравнения: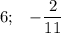
Объяснение:
Требуется решить уравнение:
Так как переменная в знаменателе, необходимо определить ОДЗ:
х + 1 ≠ 0 ⇒ х ≠ -1
х - 2 ≠ 0 ⇒ х ≠ 2
х ≠ 0.
Перенесем слагаемые из правой части в левую часть, поменяв знаки на противоположные:
Приведем к общему знаменателю и раскроем скобки в числителе:
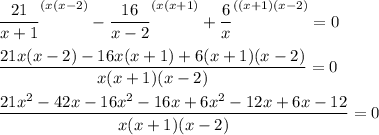
Дробь равна нулю, если числитель равен нулю.Приведем в числителе подобные члены и приравняем к нулю.
Найдем дискриминант:
√D = √4624 = 68
Теперь найдем корни:
Корни уравнения: