1. Алгебра
  2. Между городом А и Б

Между городом А и Б 280 км. Из города А в город Б выехал автомобиль. Из города Б выехали два автобуса, первый в сторону города А, второй в противоположную от города А сторону. Через 2 часа первый автобус с автомобилем встретились. Ещё через 5 часов автомобиль встретился со вторым автобусом. Какая скорость у автомобиля?

NAREK097 NAREK097    3   22.06.2021 11:17    2

Ответы
rozhkoff rozhkoff  22.07.2021 12:15

Пусть скорость автомобиля равна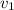 v_1, а скорость автобусов v_2.

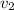Первое событие: «Через 2 часа первый автобус с автомобилем встретились».

Если тела движутся навстречу друг другу, То их скорости складываются:

(v_1+v_2) \cdot t=S\\(v_1+v_2) \cdot 2=280\\v_1+v_2=140

Второе событие: автомобиль догнал автобус через 2+5=7 часов.

Если транспортное средство едет вдогонку, то от его скорости отнимается скорость «убегающего»:

(v_1-v_2) \cdot 7=280+7v_2

(В правой части выражения — 280 км + то расстояние, которое успел проехать автобус за 7 часов)

7v_1-7v_2=280+7v_2\\v_1-v_2=40+v_2\\v_1-2v_2=40

Объединим уравнения первого и второго событий в систему:

\begin{cases}v_1+v_2=140\\v_1-2v_2=40\end{cases}

Отнимем от первого уравнения второе:

3v_2=100\\v_2=\dfrac{100}{3}\\v_1=140-v_2=140-\dfrac{100}{3}=\dfrac{320}{3}=106\dfrac{2}{3}

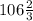ответ: 106 \frac 23 км/ч.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
rar18 rar18  12.06.2019 01:40
Решить, найти длину вектора с началом в точке a(-2,2,-1) и концом в точке b(0,3,-2)...
pollyshtal33333333 pollyshtal33333333  12.06.2019 01:40
Трое рабочих изготовили 96 деталей. первый их них изготовил в 3 раза больше деталей, чем второй, а третий-на 16 деталей больше, чем второй. сколько деталей изготовил...
Dasha07Dasha Dasha07Dasha  12.06.2019 01:40
175 под корнем скоко будет скажите !...
LiliLaind LiliLaind  12.06.2019 01:40
Как решить уравнение 2х во второй степени-5х+3...
dimalvov1993 dimalvov1993  12.06.2019 01:40
Впервом мешке было в 4раза больше моркови,чем во втором.когда из первого мешка взяли 10кг. моркови, а во второй досыпали 5кг. то в обоих мешках моркви стало поровну.ск....
albina8427 albina8427  29.10.2020 13:26
Координатор A(-3 4) B(6 5 C(5 0 D(-3 0​...
bcvfb bcvfb  29.10.2020 13:26
Вычесли значение вырожения (1/8):2^-2+(-14/15)^0+(1/6)^2•6...
Kok1n Kok1n  29.10.2020 13:26
При пересечении двух прямых, образовались углы найдите градусную меру всех углов? Если один из них равен 130 ....
ruzali4 ruzali4  29.10.2020 13:26
а) Какие значения принимает функция y =4√x , если его аргумент принимает значения из промежутка [9;16]​...
Алекс777777 Алекс777777  29.10.2020 13:26
1. Функция задана формулой у = 7x x3. Значение функции, 1) -6; 2) 8; 3) 6; 4) 8.-1, дикси:2. Графику функции, изображенному на рисунке 7, при надлежитточка с координатами:1)...

Популярные вопросы