Методом спуска решить в целых числахx^2 + 6y^2 = 5z^2

Question

Алгебра: Методом спуска решить в целых числахx^2 + 6y^2 = 5z^2​

nara01072003 · Answer

Среди всех троек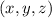 (x,y,z) , являющихся решением исходного уравнения выберем тройку 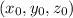$(x_{0},y_{0},z_{0})$ такую, что сумма 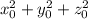$x_{0}^2+y_{0}^2+z_{0}^2$ минимальна. Если существует более одной такой тройки, то выберем любую.

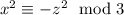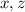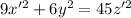Рассмотрим уравнение по модулю 3: $x^2\equiv -z^2\mod 3$ , что возможно только если x,z делятся на 3. Пусть тогда $x=3x',\;z=3z'$ . Имеем: 9x'^2+6y^2=45z'^2 , откуда ясно, что 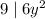$9\;|\;6y^2$ , откуда 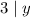$3\;|\;y$ , поэтому 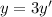y=3y' . Подставим в уравнение: 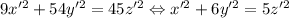$9x'^2+54y'^2=45z'^2 \Leftrightarrow x'^2+6y'^2=5z'^2$ . То есть любому решению 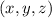(x,y,z) можно сопоставить решение 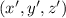(x',y',z') , причем 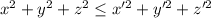$x^2+y^2+z^2\leq x'^2+y'^2+z'^2$ . Но для рассматриваемого решения сумма квадратов минимальна. 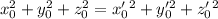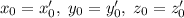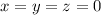Следовательно $x_{0}^2+y_{0}^2+z_{0}^2=x'_{0}^2+y_{0}'^2+z'_{0}^2$ , что возможно только в случае, если $x_{0}=x'_{0},\; y_{0}=y'_{0},\;z_{0}=z'_{0}$ , откуда следует x=y=z=0 .