Метод интервалов ( с объяснениями )

ответ:   .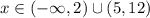

Объяснение:

Если левая часть неравенства полностью разложена на множители, то ищем нули левой части. В данном случае это х=2 , х=5 , х=12 , так как

Отметим эти точке на числовой оси и подсчитаем знаки выражения в каждом из образовавшихся интервалов, подставив любую точку из проверяемого интервала в левую часть неравенства:

Теперь выбираем промежутки, где получили знак (+), т.к. заданное неравенство имело знак ">" .