1. Алгебра
  2. M^32+(1+m^16)(1+m^8)(1+m^4)(1+m)(1-m)

M^32+(1+m^16)(1+m^8)(1+m^4)(1+m)(1-m)

ник4760 ник4760    3   18.05.2019 14:20    3

Ответы
CURTER CURTER  11.06.2020 20:48

Надо начинать применять формулу разность квадратов с двух последних скобок:

 

 m³²+(1+m¹⁶)(1+m⁸)(1+m⁴)(1+m²)(1+m)(1-m)=m³²+(1+m¹⁶)(1+m⁸)(1+m⁴)(1+m²)(1-m²)=m³²+(1+m¹⁶)(1+m⁸)(1+m⁴)(1-m⁴)=

= m³²+(1+m¹⁶)(1+m⁸)(1+m⁴)(1-m⁴)=m³²+(1+m¹⁶)(1+m⁸)(1-m⁸)=m³²+(1+m¹⁶)(1-m¹⁶)=

=m³²+(1-m³²)=1

 

 

 

 

ПОКАЗАТЬ ОТВЕТЫ
nikitastepanov21 nikitastepanov21  11.06.2020 20:48

используя формулу разности квадратов: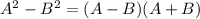 A^2-B^2=(A-B)(A+B):

 

m^{32}+(1+m^{16})(1+m^8)(1+m^4)(1+m)(1-m)=\\\\ m^{32}+\frac{(1+m^{16})(1+m^8)(1+m^4)(1+m^2)(1+m)(1-m)}{1+m^2}=\\\\ m^{32}+\frac{(1+m^{16})(1+m^8)(1+m^4)(1+m^2)(1-m^2)}{1+m^2}=\\\\ m^{32}+\frac{(1+m^{16})(1+m^8)(1+m^4)(1-m^4)}{1+m^2}=\\\\ m^{32}+\frac{(1+m^{16})(1+m^8)(1-m^8)}{1+m^2}=\\\\ m^{32}+\frac{(1+m^{16})(1-m^{16})}{1+m^2}=\\\\ m^{32}+\frac{1-m^{32}}{1+m^2}=\\\\ \frac{m^{32}(1+m^2)+1-m^{32}}{m^2+1}=\\\\ \frac{m^{34}+m^{32}-m^{32}+1}{m^2+1}=\\\\ \frac{m^{34}+1}{m^2+1}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ИЛЬЯ2161 ИЛЬЯ2161  25.08.2019 07:30
1. представьте многочлен в виде квадрата двучлена. а) 16а во 2 степени + 8аb + b во 2 степени; б) 36х во второй степени - 12х +1; в)4х во 2 степени + у во 2 степени + 4ху;...
ustinlox ustinlox  25.08.2019 07:30
При каких значениях а уравнение x(x+1)(x+2)(x+3)=a имеет не менее трех различных отрицательных корней?...
lassdeavs lassdeavs  25.08.2019 07:30
Найдите значение выражения cos2b, если 3cos2b+11sinb-7=0...
vodzinskiyaleksandr vodzinskiyaleksandr  25.08.2019 07:30
Из двух пунктов другy реки, расстояние между которыми равно 57км, навстречу друr движутся две моторные лодки. лодка, no течению, до встречи ч, a идущая лодка, идущая против...
melisa2007 melisa2007  25.08.2019 07:30
Даны две арифметические прогрессии: 1, и –10, 1, , 144. найдите количество одинаковых членов двух прогрессий...
mariii222 mariii222  25.08.2019 07:30
Решшите уравнение (3x-2)(3x+-1)(3x+3)=5...
medewwnik medewwnik  24.02.2021 11:58
EXERCISE 1 Look at the questionnaire and read the report.What are Mehmet s answers to questions 1-10in the questionnaire? очень нужно умоляю кто ответит правильно сделаю лучшим...
borodayegaliaf borodayegaliaf  24.02.2021 11:59
Составить из предложенных выражений формулы. Как можно больше. 3х, 5у, 3х, 5у, 9х 2 , 30ху, 27х 3 , 125х 2 , 15ху, 25у 2 , 125у 3 ....
misarevakin6 misarevakin6  24.02.2021 11:59
№1. Дана функция: у=-3x²-2x+7 А) запишите вершину параболы;Б) запишите ось симметрии;В) найдите точки пересечения графика с осями координат;Г) запишите промежутки возрастания...
wawking86rus wawking86rus  24.02.2021 12:00
1. Разложите на множители: 2x4 - 32 А) 2(x-4) B) 2-4 C) 20-30) D) ( 2-82x+4) E) 2(x - 2Xx + 2%x* +4) у нас сор...

Популярные вопросы