людиии не напишите какой то бред о решение этой задачи, там нужно найти геометрическую прогрессию

Yaroslava0111 2 25.11.2021 18:59 2

Question

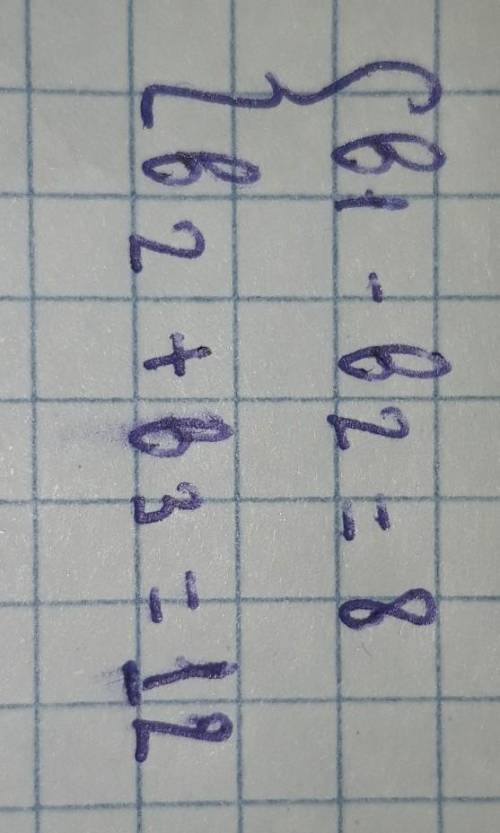
Алгебра: людиии не напишите какой то бред о решение этой задачи, там нужно найти геометрическую прогрессию

Yaroslava0111 · Answer

b1 = 16/3 = 5,33, b2 = -2,66; b3 = 1,33, q = -1/2

Объяснение:

1) Выразим b2 через b1 =>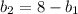 $b_{2} = 8 - b_{1}$ ;

2) Подставим во второе уравнение системы и упростим. Получится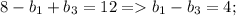 $8 - b_{1} + b_{3} = 12 = b_{1} - b_{3} = 4;$

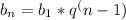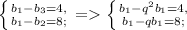
3) Запишем новую систему и разложим по формуле геометрической прогрессии: $b_{n} = b_{1} * q^(n-1)$ => $\left \{ {{b_{1} - b_{3} = 4, } \atop {b_{1} - b_{2} = 8;}} \right. = \left \{ {{b_{1} - q^2 b_{1} = 4, } \atop {b_{1} - qb_{1} = 8;}}$

4) Разделим оба уравнения друг друга т.к. b1-q*b1 не равно 0. Вынесем общий множитель, сократим, разложим числитель по ФСУ, сократим и получим знаменатель геометрической прогрессии

$\frac{b_{1} - q^2b_{1}}{b_{1} - qb_{1}} = \frac{4}{8} = \frac{b_{1}(1 - q^2)}{b_{1}(1 - q)} = \frac{1}{2} = \frac{(1 + q)(1 - q)}{(1 - q)} = \frac{1}{2} = 1 + q = \frac{1}{2};\\q = -\frac{1}{2}$

5) Подставив q в последнюю систему, отсюда получим, что b1 = 16/3 = 5,33, b2 = -2,66; b3 = 1,33

людиии не напишите какой то бред о решение этой задачи, там нужно найти геометрическую прогрессию

Популярные вопросы