1. Алгебра
  2. Логарифмическое уравнение и

Логарифмическое уравнение и неравенство. с объяснением, а то мотемотичка убьет

oksana1111156970 oksana1111156970    1   16.06.2019 04:36    2

Ответы
Яяяячччч Яяяячччч  02.10.2020 02:34

1)\; \; log_{10}(2-x)=log_{10}(x-6)\; \; ,\; \; \; ODZ:\; \left \{ {{2-x0} \atop {x-60}} \right. \; \left \{ {{x6}} \right. \\\\.\; \; \; ////////\; (2)---(6)\; ////////

Промежутки не пересекаются, значит система уравнений не имеет решений и, следовательно, уравнение не будет иметь решений.

P.S.  Даже, если не обращать внимание на ОДЗ, и записать:

2-x=x-6\; \; \to \; \; 8=2x\; \; \to \; \; x=4\; ,

то при проверке  получим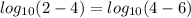  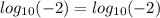log_{10}(2-4)=log_{10}(4-6)  ,  log_{10}(-2)=log_{10}(-2)  . Но логарифмы от отрицательных аргументов не имеют смысла. Значит уравнение не имеет решений.

2)\; \; log_3x+log_x(x+2)=1\; \; ,\; \; \; ODZ:\; \left \{ {{x0} \atop {x+20}} \right.\; \left \{ {{x0} \atop {x-2}} \right.\; \to \; \; x0\\\\log_3x(x+2)=log_33\\\\x^2+2x=3\\\\x^2+2x-3=0\; \; \to \; \; x_1=-30\\\\Otvet:\; \; x=1\; .\\\\\\3)\; \; log_7(2x-1)0\; \; ,\; \; x\frac{1}{2}\\\\log_7(2x-1)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
salazarcpt salazarcpt  24.06.2019 22:20
Надо решить уравнение lg(2x+1)=0.5 lg(1-3x)...
Five11 Five11  10.03.2021 09:41
Для яких значень х значення дорівнюють один одному​...
ленусиклд ленусиклд  10.03.2021 09:43
С ГРАФИКОМ ФУНКЦИИ НУЖНО СДЕЛАТЬ ТАБЛИЦУ И САМ ГРАФИК y=2x+2 y=2x-4 y=4x-1 y=5x-2...
389648 389648  10.03.2021 09:43
Выполни действия: (p2−p+4)⋅(21p2+p−4). ответ: p − p + p + p− ....
olga2610 olga2610  10.03.2021 09:44
Выпускница 11-го класса Оля решила, что хочет начать копить на планшет для учебы. Каждый день родители ей дают карманные деньги - 700 рублей. И она, узнав стоимость...
irarenkas irarenkas  10.03.2021 09:45
1. Упростите: а)(3х+2)2 б)(2х+3у)(2х-3у) с) (х+2)3 ​...
failbulkhin2017 failbulkhin2017  03.07.2019 08:20
Решите уравнение : 3x² + 5x- 2 = 0...
dreamsk831 dreamsk831  03.07.2019 08:20
решите уравнение (х+5)(х-4)+х^2+18=0...
marinadoren marinadoren  03.07.2019 08:20
Вбанк положили 50000 сумов. через один год вклад увеличился на p%. какой стала сумма вклада через один год...
lllviktorialll lllviktorialll  03.07.2019 08:20
Из 550 учащихся школы в референдуме по вопросу о введении ученического совета участвовали 88% всех учащихся. на вопрос референдума 75% учащихся, принявших участия...

Популярные вопросы