Логарифм. Реши уравнениe, используя метод подстановки.(с ОДЗ) пошагово
lg²x-3lgx=lgx²-4
Другие вопросы по теме Алгебра
Популярные вопросы
- Хто такі мандарини: А імператори Б сановники В чиновники Г шенші...
2 - 1. Що було основою господарювання первісних людей ? А) збиральництв...
2 - ТЕСТ ПО МУЗЫКЕ Симфоническая сюита Н. А. Римского-Корсакова по мотивам...
3 - Как решить задачу на сколько процентов увиличится площадь прямоугольник...
1 - очень надо ! обчислить: -3-(-6,9+5,8) а)2,9 б)-4,7 в)-1,9 г)3,1...
2 - Алгебра! Годовая С решениями, потом подкоплю и ещё дам...
1 - Колоны хорошо работали потому что; А.Им за это платили деньги Б.Их...
2 - сам не шарю Ярусы дубравы Распределите указанные ниже растения по...
2 - Програмне забезпечення - це...
3 - У цистерні було 850 л молока, 52% молока розлили у бідони. Скільки...
1
Найдём ОДЗ.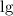 - это логарифм по основанию 10, поэтому на основание никаких ограничений не накладывается. Аргумент логарифма должен быть положительным, учитываем это условие для каждого логарифма.
- это логарифм по основанию 10, поэтому на основание никаких ограничений не накладывается. Аргумент логарифма должен быть положительным, учитываем это условие для каждого логарифма.
По свойству логарифма: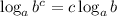 .
.
Введём замену: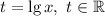 .
.
По теореме Виета:
Обратная замена:
Оба корня входят в найденную нами ранее ОДЗ, а значит, оба являются решениями уравнения.
ответ: 10; 10000.