Log(6) 5*log(5) 8+log(6) 27 объясните, как решать?
Ответы
Выучи свойства логарифмов, понимать тут особо нечего.
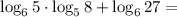
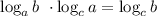
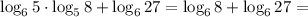
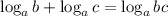
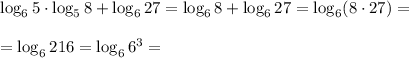
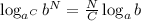
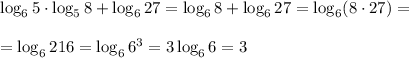
ПОКАЗАТЬ ОТВЕТЫ
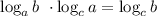
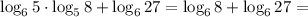
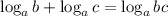
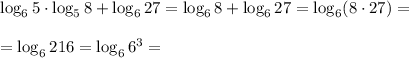
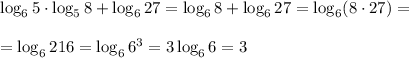
Другие вопросы по теме Алгебра
Популярные вопросы
- Радиусы окружностей равны 5 см и 3см. чему равно расстояние между их ценнтрами...
2 - Паскаль. сделайте светофор, самый простой. скиньте скрин или напишите код....
1 - Счего (каких инструментов и т. д.) фукс и хиллари пересекли континент антарктида...
2 - Some days before bonfire night they make the guy.they make him of sticks...
2 - Подберите какое-нибудь многозначное слово и напишите о нём забавную...
1 - Сдерева одновременно взлетели два орла т полетели в противоположных направлениях...
2 - Найти назовник собирают дети листья оно слетает с древ детские ладоньки...
1 - Покажите на двух- трех примерах, что окончание , суффикс и приставка действительно...
1 - Решите уравнение с росписью, чтобы понятно было 1+(x-1/2)+(x/3)+1=x...
2 - Всем доброго времени ! , проболели с ребенком месяц, не можем понять как...
2