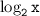Log^2 2 x-5log2x+6=0 (там логарифм в квадрате по основанию 2 числа x)
Другие вопросы по теме Алгебра
Популярные вопросы
- Музыка какого исполнителя через 200 лет будет современной? почему?...
3 - Можно ли опрадать жестокость по отношению к близкому?...
3 - В1 в каком городе ярославна молится о игоря и воинов. какую роль играет этот...
3 - 25 ! известного советского мультика «38 попугаев» мартышка и попугай решили...
3 - Написать сочинение на теиу: как жить без телефона ....
3 - Объяснить почему мы выбрали тему пословицы о дружбе?...
3 - Тело перемещалось из точки (0; 1) в точку (3; -3). определите проекцию вектора...
1 - Запиши семицифрове число й найбільше шестицифрове.на скільки одиниць перше...
2 - Как найти массу одногородного рычага,если известно масса детали на рычаге,которая...
1 - Если бы гитлер взял москву, он бы мог выиграть войну, обретя столь важный стратегический...
2
ОДЗ: под логарифмическое выражение принимает положительные значения, то есть x>0
Решим уравнение как квадратное уравнение относительно