Квадрат суммы двух последоватльных натуральных чисел больше суммы их квадратов на 840. найдите эти числа. (по ! )
Другие вопросы по теме Алгебра
Популярные вопросы
- Какие структуры входят в состав вестибулярного аппарата? 1) улитка 4)...
3 - Написать -рассуждение на тему „я читатель...
1 - Откройте скобки и поставьте в правильном времени: 1)we (go)for a walk...
2 - Переведите 1510 минут в часы с минутами, ....
3 - Поезд был в пути 3ч. и км. за первый час он км 500м,за второй час на 6...
1 - Что князь владимир мономах сделал для руси...
2 - Куда падает ударение в словах: под окном, отвечало, видало, князья, лебеди....
2 - Влотерее разыгрывалось 20 телефонов , 30 магнитофонов и 40 фотоаппаратов....
2 - Из пункта m в пункт n выехал автобус. через полчаса из n в m со скоростью,превышающей...
1 - Вес легковой автомашины равен 90 кн. площадь опоры каждого колеса равна...
1
Составим уравнение из условий задачи
n - меньшее натуральное число. Тогда n2 + (n+1)2 + 840 = ( n + n + 1)2
Раскрываем скобки.
Получаем
n2+n2+2n+1 +840 = 4n2+4n+1
или
n 2 + n - 420 = 0
D = b 2 - 4ac = 1681
√D = 41
уравнение имеет два корня n = 20 и n = - 21
Так как n - натуральное, то
ответ n = 20, m = 21
Пусть эти числа х и х+1(т.к. они последовательные).
Значит квадрат суммы равен: (х+ х+1)²= (2х+1)².
А сумма квадратов равна х² + (х+1)².
Квадрат суммы больше суммы квадратов на 840, значит их разность равна 840 или :(2х+1)² - (х² + (х+1)²)=840 . Раскроем скобки и решим уравнение:
4х² + 4х + 1 - х² - (х+1)²=840;
3х² + 4х -(х+1)² = 840-1;
3х² + 4х - х² -2х -1 = 839;
2х² -2х = 840;
х² - х = 420;
х² - х - 420=0. Квадратное уравнение
D= 1 - 4 * (-420 )= 1 + 1680=1681 = 41²
х₁=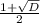 =
= 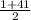 = 21.
= 21.
х₂ < 0 , значит посторонний корень.
Тогда первое число равно 21. а второе 22(т.к. они последовательные)
ответ: 21 и 22.