Кто вторым напишет верное решение, получит еще и "лучший ответ" : ) дана последовательность натуральных чисел , причем , x1 не делится на 5, а для всех остальных членов существует формула где - последняя цифра числа . доказать, что среди членов последовательности бесконечно много степеней двойки.

По условию посдедняя цифпа числа х1 не 0 и не 5 (иначе делится на 5), а значит цифра y1 равно либо 1,2,3,4,6,7,8 или 9, тогда последняя цифра числа х2 а значит и число y2 равны либо 2, 4, 6, либо 8

Так как ..2+2=...4;

...4+4=..8

..6+6=...2

...8+8...=6

то последовательность y2, y3,y4, .... является периодичной с периодом 4.

Поэтому для любого n>1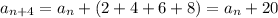

а для любого t>1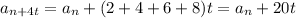

Любое число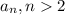 получается имеет вид

либо  либо либо где m -некоторое неотрицательное целое число

С двух членов последовательност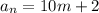и  и 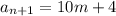  хотя бы одно делится на 4. Запишем его в виде

a_n=4l

Тогда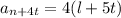

Среди чисел вида l+5t бесконечно много степеней двойки так как остатки от деления на 5 степеней двойки образуют переодическую последовательность 1,2,4,3,1, ...   и значит , бесконечно много степеней двойки дают при делении на 5 такой же остаток, как и число l