Кто-нибудь объясните... С объяснием,я не понимаю как
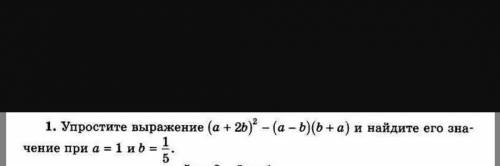
Другие вопросы по теме Алгебра
Популярные вопросы
- Подберите к слов ( словосочетание ) синоним с -не. напиши их слитно...
1 - Cd и ef-перпендикулярные прямые ,угол аов= 90 градусов угол аоf...
1 - 50 .напишите условию и решение: из города выехала фура со скоростью...
1 - Выполни действия с величинами 1 л -99 см3...
1 - По восемь примеров plants and trees- animals- fish and reptiles-...
2 - Где в казахстане встречаются амфибии?...
1 - Определить знак: а)sin210 б) tg300 в) cos300 г) ctg73 д) sin190...
2 - Сума нескінченної ї прогресії =72,знаменник =1: 3,другий член...
1 - При каких значениях у выражения 0,6-у/9 и 13-у/4,5 будут равны...
2 - Эссе на тему мой любимый актер . про знаменитых)) заранее ))...
2
(a+2b)²-(a-b)(b+a)= a²+ 4ab + 4b² - (a²-b²) = a² + 4ab + 4b² -a² +b²
сокращаем
4ab+5b²
при a=1; b=⅕ 4ab+5b²= 4×1×0,2 + 5×0,2² = 0,8 + 0,2 = 1
Объяснение:
в первоначальном выражении присутствуют 2 формулы сокращённого умножения, мы раскрываем скобки, но перед скобкой (a²-b²) стоит минус, значит мы меняем знаки внутри скобки. Потом сокращаем похожие множители (a²-a²),(4b²+b²), а 4ab остаётся самостоятельно. То есть получается 4ab+5b². Подставляем числа и прорешиваем.
4ab+5b²;
при a=1; b=⅕ ответ: 1
Объяснение:
(a + 2b)²- (a - b)(b + a) = a²+ 4ab + 4b² - (a²- b²) = a² + 4ab + 4b² - a² +b²
взаимоуничтожаем a² и -a², приводим подобные члены и получаем: 4ab+5b²
при a=1; b=⅕ 4ab+5b²= 4×1×0,2 + 5×0,2² = 0,8 + 0,2 = 1
В выражении присутствуют формулы квадрат суммы и разность квадратов, раскрываем скобки, с учётом знаков перед скобкой, в данном случае "-", следовательно, все знаки внутри скобок меняем на противоположные. Потом взаимоуничтожаем a² и -a², приводим подобные члены и получаем 4ab+5b². Далее находим значение выражения 4ab+5b², при установленных значениях, для этого подставляем числа в полученное выражение и решаем.