Користуючись означенням, знайдіть похідну функції:
f(x) = 5х^2 + 1;
Другие вопросы по теме Алгебра
Популярные вопросы
- Диагонали граней прямоугольного параллелепипеда равны 7см, 8см,...
3 - Вселе пряничном дома построены из 1852 пряников.из них медовых пряников...
3 - Какой корень в слове ромашка какое проверочное слово к слову счастлива...
1 - Длина прямоугольника 12 см,ширина состовляет одну вторую длины.чему...
2 - Построить график уравнений xв второй степени+y в второй степени=16...
2 - Выражение вектор 1.ав+ вектор вс 2. вектор мn+вектор ке+вектор nk...
2 - Всаду растут 10 грушевых деревьев,что составляет 2/5 всех деревьев...
1 - Расскажи о битве на куликовом поле. в своем рассказе используйте...
3 - Составить 2-3 предложения связанные между собой о том как я изучаю...
3 - 4м2дм+(6м8дм-100см) выразить в метрах...
2
Означення похідної:
Отже, за означення, похідна функції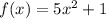 дорівнює
дорівнює 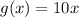 .
.