Корень (3-х/х-1) +3корень(х-1/3-х)=4

Уравнение содержит корни, значит первым делом необходимо найти область определения :

∈ ()

Примем выражние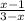 за t , тогда 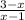= 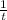, тогда наше уравнение выглядит так :

Возводим в квадрат :

Решаем квадратное уравнение и находим корни :

Делаем обратную замену :

Решаем систему и находим корни :

Оба корня удовлетворяют области определения, значит уравнение решено.