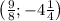Координаты вершины параболы, заданной уравнением y = 4x² - 9x + 1 с подробным решением
Другие вопросы по теме Алгебра
Популярные вопросы
- Нужно найти диктант по , 8 класс называется город-герой диктант про севастополь,помню...
1 - Дано выражение 7z/f=8 если из него выразить f то получиться выражение...
3 - Вкаком году король нормандии взял власть во франции...
1 - Найти правильный вариант ответа,...
2 - Поміркуйте чому досить розвинені цивілізації ацтеків майя та інків так стрімко...
3 - Ученик прочитал 35 страниц. это составляет 17,5% книги. сколько страниц в...
3 - Если на объективе свеового микроскопа указано ×4 а на окуляре ×10 то на таком...
3 - Письмо нужно доклад как и где появился и тд...
3 - Написать диалог о достопримечательности 10 реплик 45 !...
3 - На субботник вышли 160 человек.в ремонте дороги участвовали 25%всех людей,...
2
Абсцисса вершины параболы равна по формуле
В данном случае b=-9, a=4.
Это случай, когда дискриминант равен 0. То есть первое и второе решения совпадают.
Ординату узнаем, подставив абсциссу в само уравнение кривой
Координаты вершины параболы