Коло заданої рівнянням х^2+у^2=9. Визначте координати точки, яка належить кругу, обмеженому цим колом.

Объяснение:

 Уравнение окружности радиуса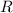 с центром в точке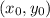

 Сравнивая это уравнение с исходным, делаем вывод, что

Чтобы найти координаты точки, которая принадлежит кругу, образованного уравнением x^2 + у^2 = 9, мы должны использовать уравнение круга. В данном случае радиус круга равен 3, так как квадраты коэффициентов x и у равны 1.

Для нахождения координат точки, можно выбрать любое значение для одной из переменных и подставить его в уравнение. Затем можно найти вторую переменную, основываясь на значении, которое мы выбрали для первой переменной.

Давайте рассмотрим несколько примеров для нахождения координат точек:

1. Пусть x = 0. Подставим значение в уравнение:
0^2 + y^2 = 9
y^2 = 9
y = ±√(9)
y = ±3

Таким образом, получаем две точки: (0, 3) и (0, -3).

2. Пусть у = 0. Подставим значение в уравнение:
x^2 + 0^2 = 9
x^2 = 9
x = ±√(9)
x = ±3

Таким образом, получаем две точки: (3, 0) и (-3, 0).

3. Выберем некоторое другое значение для x, например, x = 1. Подставим значение в уравнение:
1^2 + y^2 = 9
y^2 = 8
y = ±√(8)
y ≈ ±2.828

Таким образом, получаем две точки: (1, 2.828) и (1, -2.828).

4. Выберем некоторое другое значение для у, например, у = 2. Подставим значение в уравнение:
x^2 + 2^2 = 9
x^2 = 5
x ≈ ±√(5)

Таким образом, получаем две точки: (√(5), 2) и (-√(5), 2).

Таким образом, координаты точек, которые принадлежат кругу, образованного уравнением x^2 + у^2 = 9, будут:
(0, 3), (0, -3), (3, 0), (-3, 0), (1, 2.828), (1, -2.828), (√(5), 2), и (-√(5), 2).