Кли­ент а. сде­лал вклад в банке в раз­ме­ре 3800 руб­лей. про­цен­ты по вкла­ду на­чис­ля­ют­ся раз в год и при­бав­ля­ют­ся к те­ку­щей сумме вкла­да. ровно через год на тех же усло­ви­ях такой же вклад в том же банке сде­лал кли­ент б. ещё ровно через год кли­ен­ты а. и б. за­кры­ли вкла­ды и за­бра­ли все на­ко­пив­ши­е­ся день­ги. при этом кли­ент а. по­лу­чил на 418 руб­лей боль­ше кли­ен­та б. какой про­цент го­до­вых на­чис­лял банк по этим вкла­?

Формула сложной процентной ставки: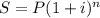

где S - наращенная сумма (сумма которую получит клиент через n лет), P - сумма вклада, i - процентная ставка(годовых), n - срок.

Клиент А положил в банк 3800 рублей, тогда через год он получит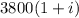 рублей. В тех же условиях через год клиент Б получит 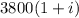рублей, в это же время два года для клиента А, он должен получить 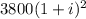рублей. Зная, что клиент А получил на 418 рублей больше клиента Б, составим уравнение:

Решаем как квадратное уравнение относительно (1+i)

i₁ < 0 т.е. оно не удовлетворяет условию;

Т.е. под 10% годовых начислял банк по этим вкладам.

ответ: 10 %.