Касательная к графику функции y=4e^(3x) -7x параллельна прямой y=5x-1 найдите абсциссу точки касания

Question

Алгебра: Касательная к графику функции y=4e^(3x) -7x параллельна прямой y=5x-1 найдите абсциссу точки касания

МАРИШКАНИК · Answer

По геометрическому смыслу производной: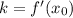 k=f'(x_0)

Производная функции:

$f'(x)=(4e^{3x}-7x)'=4e^{3x}\cdot (3x)'-7=12e^{3x}-7$

Касательная параллельна прямой y = 5x-1, а у параллельных прямых угловые коэффициенты равны, т.е. k=5. Подставляем в геометрический смысл производной.

$5=12e^{3x_0}-7\\ 12e^{3x_0}=12\\ e^{3x_0}=e^0\\ 3x_0=0\\ x_0=0$

Абсцисса точка касания равна x₀ = 0

Касательная к графику функции y=4e^(3x) -7x параллельна прямой y=5x-1 найдите абсциссу точки касания

Популярные вопросы