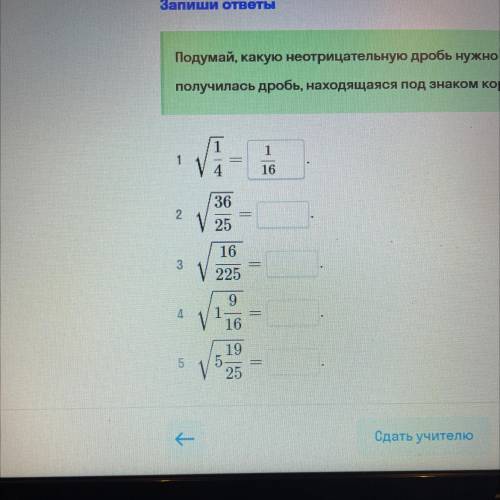
Какую неотрицательную дробь нужно возвести в квадрат, чтобы получилась дробь, находящаяся под знаком корня, см. фото

Чтобы найти неотрицательную дробь, которую нужно возвести в квадрат, чтобы получилась дробь, находящаяся под знаком корня, мы должны использовать обратную операцию квадратного корня, которой является возведение в квадрат.

На фотографии виден корень из некоторой дроби, а это значит, что мы должны найти такую дробь x, которая возводится в квадрат и равна данной дроби.

Давайте решим эту задачу с пошаговым объяснением:

1. Начнем с того, что записываем данную нам дробь под знаком корня: √(a/b).

2. По определению корня, мы должны найти такое число x, что x^2 = a/b.

3. Чтобы избавиться от корня, возведем обе части уравнения в квадрат: (x^2)^2 = (a/b)^2.

4. На левой стороне уравнения операция возведения в квадрат отменяется, и мы получаем x^4 = (a/b)^2.

5. Далее мы можем записать (a/b)^2 в виде a^2/b^2, чтобы упростить уравнение: x^4 = a^2/b^2.

6. Чтобы избавиться от неизвестной дроби, умножим обе части уравнения на b^2: b^2 * x^4 = a^2.

7. Полученное уравнение b^2 * x^4 = a^2 означает, что мы должны найти значение x, чтобы b^2 * x^4 равнялось a^2.

8. Поскольку нам нужна неотрицательная дробь, мы должны взять положительное значение x, иначе у нас получится отрицательная дробь под знаком корня.

9. Таким образом, необходимо возвести в квадрат дробь x = sqrt(a^2/b^2) = a/b.

Таким образом, чтобы получить дробь, находящуюся под знаком корня, нужно возвести в квадрат дробь a/b.