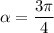Какой угол составляет касательная к графику функции y=x^2+3x+4 в точке с абсциссой x0=-2,с положительным направлением оси ox? ​

Найдем уравнение касательной, проходящей через точку с абсциссой

Для этого найдем производную данной функции:

Найдем значение функции в точке с абсциссой :

Найдем значение производной данной функции в точке с абсциссой :

Уравнение касательной имеет вид:

Подставим значение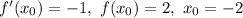

Итак, уравнение касательной заданной функции: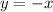

Воспользуемся геометрическим смыслом касательной: коэффициент наклона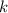 касательной 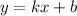численно равен тангенсу угла наклона  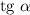с положительным направлением оси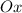

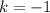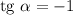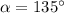В найденной касательной коэффициент , следовательно, при или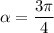

ответ: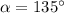 или