Какой степени это уравнение 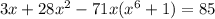 ?
?
Другие вопросы по теме Алгебра
Популярные вопросы
- Вычислите: 5,8 в квадрате - 3,8 в квадрате дробная черта 9,8...
2 - Сам с а слов с горшок. на глубже вспашешь -пять дней засухи перенесёшь....
1 - Реши уравнение: ( 7,5 + икс) -2,94= 5,67...
2 - Представители высших растений. ( конкретно название)....
3 - Самостоятельно прокомментируй выделенные слова. тут он было вышел,...
1 - Маша неплотно закрыла кран на кухне в 7 часов 20 минут и ушла в школу....
1 - Решить уравнение, совсем запуталась со знаками: 5-2(x-1) + 3(x-2)=0...
3 - Какие растения занесены в красную книгу украины?...
1 - Установите соответствие между классом растений и его представителем:...
2 - А.и. «куст сирени», «аllez». характеристика главных героев (одного...
1
Для начала, чтобы определить степень данного уравнения, мы должны выяснить, наибольшую степень переменной x, которая присутствует в уравнении.
В данном случае, мы видим, что в уравнении присутствуют такие слагаемые как 3x, 28x^2, -71x и x^6. Нам нужно найти наибольшую степень переменной x среди всех этих слагаемых.
Посмотрим на каждое слагаемое по отдельности:
1) В слагаемом 3x, переменная x имеет степень 1, так как x возводится только в первую степень.
2) В слагаемом 28x^2, переменная x имеет степень 2, так как x возводится во вторую степень.
3) В слагаемом -71x, переменная x имеет степень 1, так как x возводится только в первую степень.
4) В слагаемом x^6, переменная x имеет степень 6, так как x возводится в шестую степень.
Итак, мы видим, что наибольшая степень переменной x в этом уравнении равна 6.
Теперь можем сказать, что данный многочлен имеет степень 6, так как это наибольшая степень переменной x, присутствующей в уравнении.
Важно заметить, что уравнение и многочлен - это два разных понятия. Многочлен - это выражение, состоящее из слагаемых, содержащих переменные с определенными степенями. А уравнение - это выражение, содержащее знак равенства и одну или несколько переменных. В данном случае, мы говорим о степени многочлена, который задан уравнением.
Надеюсь, что объяснение было понятным и осветило эту тему для тебя. Если у тебя еще остались вопросы, не стесняйся задавать их. Я всегда готов помочь!