1. Алгебра
  2. Какое наименьшее значение может

Какое наименьшее значение может принимать выражение а+(b-c)/d для попарно различных чисел а, b, c, d из набора 2, 3, 4, 5, 6, 7, 8, 9?

seryakovart seryakovart    1   21.03.2020 10:05    3

Ответы
Dinochka99 Dinochka99  12.10.2020 01:58

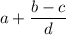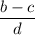Рассмотрим выражение a+\dfrac{b-c}{d}. Чтобы оно было наименьшим, необходимо, чтобы выражения a и \dfrac{b-c}{d} были наименьшим.

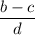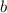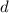Заметим, что выражение \dfrac{b-c}{d} может быть отрицательным. Если его числитель будет наименьшим отрицательным, а знаменатель - наименьшим положительным, то оно примет наименьшее значение. Значит, b необходимо выбрать наименьшим, c - наибольшим, d - наименьшим.

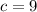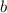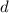Наибольшее c=9. Наименьшие значения 2, 3, 4 нужно распределить между выражениями a, b и d. Проверим все варианты.

Пусть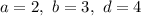 a=2,\ b=3,\ d=4. Тогда: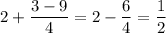 2+\dfrac{3-9}{4}=2-\dfrac{6}{4}=\dfrac{1}{2}

Пусть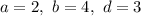 a=2,\ b=4,\ d=3. Тогда: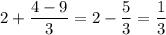 2+\dfrac{4-9}{3}=2-\dfrac{5}{3}=\dfrac{1}{3}

Пусть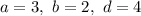 a=3,\ b=2,\ d=4. Тогда: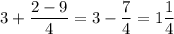 3+\dfrac{2-9}{4}=3-\dfrac{7}{4}=1\dfrac{1}{4}

Пусть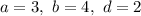 a=3,\ b=4,\ d=2. Тогда: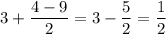 3+\dfrac{4-9}{2}=3-\dfrac{5}{2}=\dfrac{1}{2}

Пусть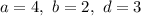 a=4,\ b=2,\ d=3. Тогда: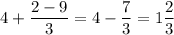 4+\dfrac{2-9}{3}=4-\dfrac{7}{3}=1\dfrac{2}{3}

Пусть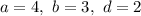 a=4,\ b=3,\ d=2. Тогда: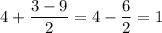 4+\dfrac{3-9}{2}=4-\dfrac{6}{2}=1

Наименьшее значение равно 1/3.

ответ: 1/3

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Dogi2008 Dogi2008  20.03.2019 10:00
Умоляю класс контрольная работа...
poliaprokopets poliaprokopets  20.03.2019 10:00
Решите пример, он легкий, с решением . много...
ilya1613 ilya1613  20.03.2019 11:00
Выполните действия: 1) (-7b^2 - b + ) 2) 0.5a(2a - b) - 0.5b(2b - a)...
olgabykova2006 olgabykova2006  20.03.2019 11:00
При каких значениях х имеет смысл выражения? корень квадратный из (2х-5)(х-17)?...
1Ліночка1 1Ліночка1  20.03.2019 10:03
X^2y+xy^2-2-x-y+2xy нужно разложить на множители...
Лубничка Лубничка  20.03.2019 11:00
Преобразуйте в многочлен а) (1+х)(1-х)(1+хх)...
060609 060609  20.03.2019 10:05
Найдите 14 член арифметической прогрессии (an) если a первое =2 и а второе =5...
Aloyna111 Aloyna111  20.03.2019 11:00
Какое из данных чисел является иррациональным? (√3 ) в 5 степени? или дробь √ 5 целых четере девятых ( вся дробь под корнем)...
slavik116 slavik116  20.03.2019 10:08
После уценки на 20% ноутбук стал стоить 21000 рублей. сколько рублей стоил ноутбук до уценки?...
Il123456 Il123456  20.03.2019 11:00
С. надо( 1 область значений y=5-3cosx 2 нули функции y=0,2sin(пи/3-3/2x) 3 промежутки монотонности y=5tg(3x-пи/3)...

Популярные вопросы