Какие из чисел входят в область допустимых значений алгебраической дроби 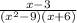$\frac{x - 3}{( {x}^{2} - 9)(x + 6)}$
Верных ответов: 3
1)3
2)-6
3)6
4)0
5)-3
6)9

Ответы

wEnD11 02.04.2021 12:10

Числитель данной дроби не равен нулю, так как на ноль делить нельзя.

Решим следующее уравнение и откинем лишние корни:

$(x^{2} -9)(x+6)\neq 0$

Произведение двух чисел равно нулю, когда один из множителей равен 0, значит:

$(x^{2} -9)\neq 0\\$

$x^{2} \neq 9\\x1\neq 3\\x2\neq -3$

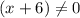
или $(x+6)\neq 0\\$

$x\neq -6$

Значит корни 3, -3, -6 не входят в область определения.

ответ: 3) 4) 6)

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

fyjdtjjhtjh 20.09.2019 23:20

asya1607 20.09.2019 23:20

0,25 + 0,1 (х+0,5) = 0,4х решите уравнение...

АружанТопская 20.09.2019 23:20

Докажите, что 2^22+2^21-2^19 делится на 11...

4кпнигш 20.09.2019 23:20

Silwashka99 21.08.2019 08:10

(3a-2)(3a+2) преобразовать в многочлен...

нурбол5 21.08.2019 08:10

milena7772 21.08.2019 08:10

Исследуй функцию на четность 1+sinx/1-sinx...

foxtrot2910 21.08.2019 08:10

wonderr 21.08.2019 08:10

СофикоПримудрая 21.08.2019 08:10

(4a-x)(16a^2-4ax+x^2)-64a^3+x^3 при a=1,x=-1 20...

Какие из чисел входят в область допустимых значений алгебраической дроби Верных ответов: 31)32)-63)64)05)-36)9 ​