1. Алгебра
  2. Как решить? cos π / 12 + sin

Как решить? cos π / 12 + sin 7π / 12 .Желательно с формулой по которой решали и с формулой разности.

maksarowa1980 maksarowa1980    3   01.04.2020 21:44    0

Ответы
Yuliya12222222222 Yuliya12222222222  12.10.2020 12:34

\cos\frac{\pi}{12}+\sin\frac{7\pi}{12}=\cos\frac{\pi}{12}+\cos(\frac{\pi}{2}-\frac{7\pi}{12})=\cos\frac{\pi}{12}+\cos\frac{\pi}{12}=2\cos\frac{\pi}{12};

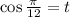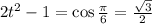Пусть \cos\frac{\pi}{12}=t, тогда 2t^{2}-1=\cos\frac{\pi}{6}=\frac{\sqrt{3}}{2}; Из определения следует, что 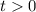t0; Из уравнения получаем: 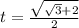t=\frac{\sqrt{\sqrt{3}+2}}{2}; Итоговый ответ: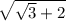 \sqrt{\sqrt{3}+2}

ПОКАЗАТЬ ОТВЕТЫ
кузя1310 кузя1310  12.10.2020 12:34

\frac{\sqrt{2} +\sqrt{6} }{2}

Объяснение:

1) π/12+π/2=(π+6π)/12=7π/12

2) π/3-π/4=(4π-3π)/12=π/12

3) cos(α-β)=cosαcosβ+sinαsinβ

sin\frac{7\pi }{12} =sin(\frac{\pi }{12}+\frac{\pi }{2} )=cos\frac{\pi }{12} \\cos\frac{\pi }{12} +sin\frac{7\pi }{12}=2cos\frac{\pi }{12}=2cos(\frac{\pi }{3}-\frac{\pi }{4})=2(cos\frac{\pi }{3}cos\frac{\pi }{4}+sin\frac{\pi }{3}sin\frac{\pi }{4})=\\=2(\frac{1}{2}.\frac{\sqrt{2} }{2} +\frac{\sqrt{3} }{2}.\frac{\sqrt{2} }{2})=\frac{\sqrt{2} +\sqrt{6} }{2}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
tttyadoyan235 tttyadoyan235  23.08.2019 14:10
Выражение -0,1x (2х2 + 6) (5 - 4х2)....
Nalalisa Nalalisa  23.08.2019 12:22
7класс решить систему уравнений...
gimazova99 gimazova99  23.08.2019 12:20
Доведіть нерівність: 2x²-4xy+4y²+6x+9≥0...
liusen liusen  23.08.2019 12:13
Обчисліть площу фігури обмеженої графіком y= cos x і прямими y=0 x= 0 x= п/3...
Sofff24 Sofff24  16.02.2021 12:51
1. Два мяча подбросили вертикально вверх, и они упали на землю. На рисунке 21 изображены графики зависимостивысоты расположения мячейнад землей от времени полета.Используя графики,...
indyk1 indyk1  16.02.2021 12:57
Напишите функции к этим графикам функции...
Keks200220 Keks200220  23.12.2020 14:55
5.) Укажіть графік функції у = -/х ул.у22.у2222.- 2б)B)B)a)​...
султа65 султа65  23.12.2020 14:55
АЛГЕБРА из пункта A выехал велосипедист, а через 45 минут выехал мотоциклист,обогнавший велосипедиста на расстоянии 15 км от пункта AНайти V велосипедиста и мотоциклиста,если...
KaKOYTAGHOM KaKOYTAGHOM  23.12.2020 14:56
А)42+50-18+27 б)144-525010 2.x=-4+5 3. Сократите дробь 3-3 a-3 --------------------------- ----------------------------------------------------- 23 a-3 x-2x+1 -------------------------------------...
alti1997 alti1997  23.12.2020 14:56
Найти нули функции y= 2,2x + 10...

Популярные вопросы