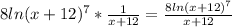Как найти производную (ln(x+12)⁸)' =?
не могу понять
Другие вопросы по теме Алгебра
Популярные вопросы
- Героический характер Тараса Бульбы № п/п Черта характера При каких...
1 - Карточка ради бога кому не сложно...
1 - ЭПАМАГИТ ЖАЗЫЛЫМ АЙТЫЛЫМ 8-тапсырма.Өлеңдегі әр қызға ат қой.Ол қызды...
3 - Якщо хвиля переходить з одного середовища в інше що буде з швидкістю,...
1 - Найди площадь каждой фигуры...
2 - Розкрийте зміст одного з прислів’їв. У відповіді вживайте складнопідрядні...
3 - Выберите координаты той территории, которую исследовал Н.М. Пржевальский....
2 - Привет как дела поздравляю с 3 четверти ...
3 - 309 Прочитайте сначала текст без слов, данных в скобках, потом - с...
2 - синтаксический разбор предложения: И вот более 100 лет назад люди...
2
Объяснение:
Тут производная сложной функции. За g берём ln(x+12).
По формуле (f(g))'=f(g)*g'
Производная от (g^8)' = 8g^7
Производная от (ln(x+12))' тоже сложная функция. ln(g)'*(x+12)'=(1/g)*1
Обратная замена: g=x+12→ 1/(x+12)
Заменяем g= ln(x+12), получаем: